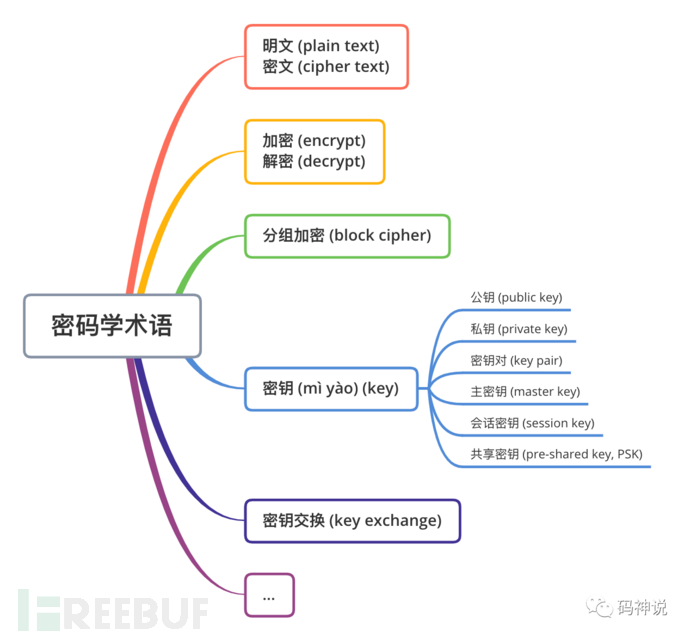
• 导读

• 密钥与加密算法

• 对称加密

• 非对称加密

• 加密速度测试

• 混合加密

• 参考

1 导读

密码学（cryptography）是一门研究如何隐密地传递信息的学科，是数学和计算机科学的分支。
在近代以前，密码学只考虑到消息的机密性，即如何将可理解的消息转换成难以理解的消息，并且使得收到机密消息的人能够逆向恢复。近数十年来，这个领域已经扩展到涵盖身份认证 / 鉴权（authentication）、消息完整性检查（message integrity）、数字签名（signature）、交互证明、安全多方计算等各类技术。
自工作以来，自己对于密码学的基础知识，一直是懵懵懂懂，不成体系，为此，我决心要来一次系统化的梳理，廓清迷雾。此外，也为后面介绍 WebRTC 的 DTLS-SRTP 技术做好铺垫。本文主要梳理对称加密与非对称加密的基本原理。

2 密钥与加密算法

密钥是指用来完成加密、解密、完整性验证等密码学应用的秘密信息（不能泄露），是一串非常大的数字，可以通过随机数生成器（random number generator, RNG）或伪随机数生成器（pseudorandom number generator, PRNG）随机生成。

密钥的度量单位是 “位” bit，而不是 “字节” byte。比如，密钥长度是 128 位，就是 16 字节的二进制串；密钥长度是 1024 位，就是 128 字节的二进制串。

密钥是加密算法的输入参数，加密算法使用密钥加解密，但是密钥并不是由加密算法本身生成的。

remark: 密钥与加密算法没有直接的关系，密钥实质是很大的整数，但不同的加密算法对密钥有不同的要求。比如对称加密算法 AES128，要求密钥是 128 位的整数，再如非对称加密算法 RSA1024，要求密钥是 1024 位的整数，且必须是质数，这些大整数都是由随机数生成，与加密算法无关。

我们可以用锁和钥匙来比喻加密算法中的密钥与加密算法。现实世界中的钥匙通常是具有一定形状的金属片，用来打开锁，而密码学中的 “钥匙”（密钥）则是用来 “打开” 密文。密钥就是钥匙，加密算法就是锁，上锁和开锁必须要有钥匙，而加密和解密就是上锁和开锁的动作。

机密性是信息安全的基础。实现机密性的最常用的手段是 “加密”，按照密钥的使用方式，加密可以分为两大类：对称加密和非对称加密。

3 对称加密

对称加密的 “对称” 就是指加密和解密使用同一个密钥，对称密钥又称为共享密钥（Pre-Shared key，PSK）。由于对称加密只有一个密钥，因此一定要保证密钥的安全，才能保证通信的机密性。

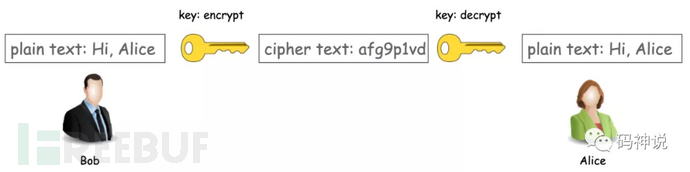
对称加密的原理很简单。比如，Bob 给 Alice 发消息，在此之前双方先约定好使用一个对称密钥，在双方通信的过程中传输的消息全是密钥加密后的密文，除了 Bob 和 Alice 之外，没有人能够解密。即使有黑客窃听，看到的也只是乱码，因为黑客没有密钥，无法解密密文，因此对称加密实现了机密性。

目前最流行的对称加密算法莫过于 AES（Advanced Encryption Standrad），中文译为 “高级加密标准”。密钥长度可以是 128，192 或 256 位。因为该算法由比利时密码学家 Joan Daemen 和 Vincent Rijmen 共同设计，所以又称 Rijndael 加密法。

note: 说到对称加密算法，不得不提一下分组加密工作模式的概念。分组加密又称为块加密，是一种对称密钥算法，它将明文分成多个等长的模块（block），使用确定的算法和对称密钥对每组分别加解密。而工作模式则是用来进行加密和认证，最早有 ECB、CBC、CFB、OFB、CTR 等几种工作模式，最新的工作模式被称为 AEAD，常用的是 GCM 和 CCM。

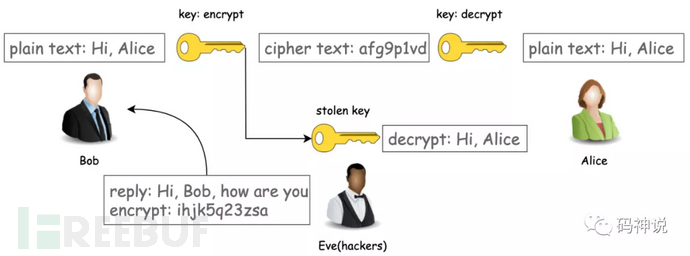
对称加密看上去实现了通信的机密性，但是却存在密钥交换的问题，即密钥如何安全的传递给对方。在上图中，我们假设黑客没有对称密钥，所以即使窃听到密文也无法解密。但是如果黑客在密钥传递的途中窃取了密钥，如下图所示，那么他就可以随意加解密收发的数据，通信过程的机密性就荡然无存了。

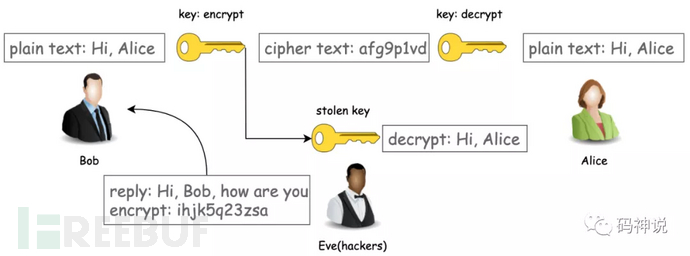
正因为对称加密无法解决密钥安全交换的问题，所以出现了非对称加密。

4 非对称加密

非对称加密也叫公钥加密算法。它的 “不对称” 在于它有两个密钥，一个叫 “公钥”，可以交付给任何人（往往通过数字证书的方式交付），另一个叫 “私钥”，必须严格保密，公钥和私钥是 “一对”，称为密钥对（key pair），且具有数学关系。

和对称加密的密钥一样，非对称加密的公钥和私钥也是都可以用来加密与解密的。不过，公钥加密后只能用私钥解密，反过来，私钥加密后也只能用公钥解密，所以，非对称加密具有 “单向” 性”。

那么，非对称加密究竟是如何解决了 “密钥交换” 的问题呢？很简单：因为非对称加密具有 “单向性”，所以公钥加密后只能用私钥解密。又因为用于密钥交换的是公钥，私钥由持有者严格保密，所以黑客是拿不到私钥的，拿不到私钥就没法解密。

举个例子，Alice 生成了一对密钥，给 Bob 和 Eve 每人一把公钥，而私钥则自己持有。这样当 Bob 和 Eve 给 Alice 发消息的时候就可以用公钥加密，Alice 则使用自己的私钥解密，因为黑客 Eve 是无法拿到 Alice 的私钥的，所以即使他窃听到密文也无法解密。

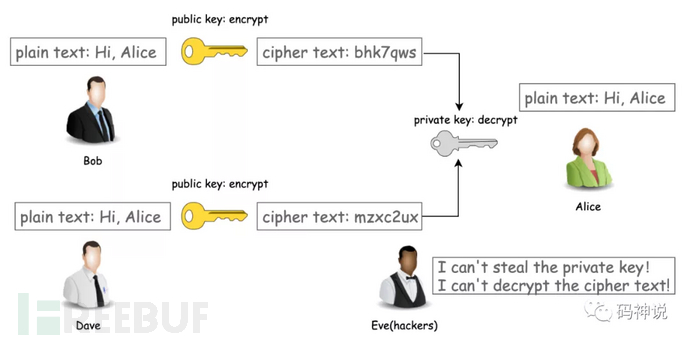
在上面的图中，我们假设 Bob 只是单向的给 Alice 发消息，因此需要 Alice 生成一对密钥对，私钥自己保存，公钥发给 Bob。那么同理，如果 Alice 要给 Bob 发消息，就需要 Bob 的公钥，所以 Bob 同样也要生成一对密钥对，私钥自己保存，公钥发给 Alice。

关于非对称加密算法，最著名的莫过于 RSA。1977 年，三位数学家 Rivest、Shamir 和 Adleman 设计了一种算法，可以实现非对称加密。这种算法用他们三个人的名字命名，叫做 RSA 算法。RSA 这种非对称加密算法应用在我们熟知的 TLS、DTLS、HTTPS、SSH 协议中。只要有计算机网络的地方，就有 RSA 算法，因此，说它是计算机通信安全的基石也不为过。

RSA 密钥长度一般取 1024 或者 2048 位 ，密钥长度越长，就越难被破解。到目前为止，世界上还没有任何可靠的攻击 RSA 算法的方式。RSA 算法的原理涉及到一些数论知识，本文就不做介绍了，感兴趣的读者可以看 这篇文章。

公钥和私钥的生成方式有很多，比如银行常见的 U 盾，就是在硬件内部生成。在 Linux/Mac 上，我们则可以使用 ssh-keygen 命令和 openssl 命令来生成 RSA 的公钥和私钥，大家可以亲自去敲一下命令，加深理解。

remark: 密钥是个很大的数字（二进制串），然而使用 ssh-keygen 或者 openssl 生成的密钥是一串很长的字符串，看起来似乎并不是数字。这是因为密钥经过了 base64 编码，将二进制数据转换为了字符串，这样就增加了密钥的可读性，便于密钥的分发，也便于用编辑器打开密钥文件后粘贴复制。而且，在计算机中，一切皆数字，所以字符串也是数字。

5 加密速度测试

既然非对称加密解决了密钥交换的问题，保证了密钥的安全性，那么是否可以用它取代对称加密呢？答案是，不能。这是因为非对称加密算法进行的都是大数运算，这使得 RSA 的速度比同样安全级别的对称加密算法要慢 1000 倍左右，这一点从 AES 和 RSA 的密钥长度的差异中就能感受到。

我用 go 写了 AES 和 RSA 加解密的代码，来对比二者的加密速度，机器配置是 mac pro 2019，6 核 16 G，程序输出结果如下图所示：

可以知道，在明文相同，加解密次数相同的情况下，RSA 的耗时是 AES 的 1270 倍。在我的 github 有完整的 加解密速度测试代码。

6 混合加密

现在，我们知道了：对称加密速度快，但是密钥交换不够安全，非对称加密保证了密钥交换的安全，但是速度又太慢。那么，有没有一种能够鱼与熊掌兼得的加密方法呢？

当然有，这就是混合加密，WebRTC 的 DTLS-SRTP 就是使用了混合加密的方式，其大致原理是：

1. 通信双方选择非对称加密算法，比如 RSA，准备进行安全的密钥交换。

2. 通信双方使用随机数生成对称加密算法的会话密钥，用公钥加密后发给对方。

3. 通信双方各自用私钥解密，得到对称加密的会话密钥。

4. 之后双方全部使用对称加密进行通信。

remark: 由于会话密钥通过非对称加密安全传输，所以很难被黑客破解。而且会话密钥一般是一次一密，是一个会话级别的随机数，所以即使被破解也只是本次会话受影响。

混合加密融合了对称加密和非对称加密两种方式，兼具了性能和安全，保证了通信的机密性，然而这并不代表绝对的安全。在上文介绍非对称加密的图中，黑客 Eve 确实是拿不到 Alice 的私钥了，但是他可以截获到 Alice 发给 Bob 的公钥，并且黑客 Eve 也可以生成一对密钥，私钥自己保存，然后把公钥发给 Alice，让 Alice 误以为这是 Bob 的公钥。也就是说黑客 Eve 对 Alice 扮演了 Bob 的角色，他的这种攻击行为称为中间人攻击。

那么，该如何解决中间人攻击的问题呢？一个核心的解决这个问题的思想是：认证消息发送者的身份，也就是证明消息确实是你发的。下一篇我会详细介绍身份认证的细节，感谢阅读。

7 参考

https://time.geekbang.org/column/article/109062 http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html
https://studygolang.com/articles/28458 https://segmentfault.com/a/1190000021267253