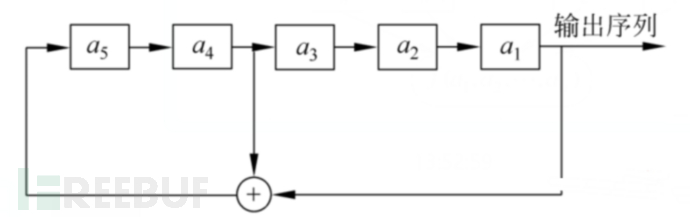
线性反馈移位寄存器(LFSR)归属于移位寄存器(FSR),除此之外还有非线性移位寄存器(NFSR)。移位寄存器是流密码产生密钥流的一个主要组成部分。
$GF(2)$上一个n级反馈移位寄存器由n个二元存储器与一个反馈函数$f(a_1,a_2,...,a_n)$组成,如下图所示。
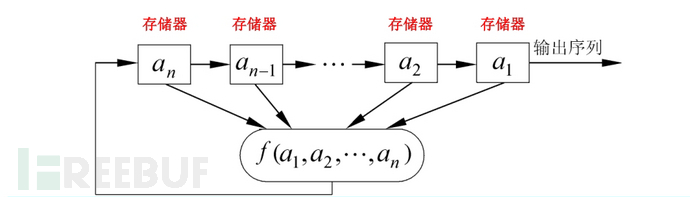
移位寄存器的三要素:
初始状态:由用户确定
反馈函数:$f(a_1,a_2,...,a_n)$是n元布尔函数,即函数的自变量和因变量只取0和1这两个可能值
输出序列
如果反馈函数是线性的,那么我们称其为 LFSR,如下图所示:
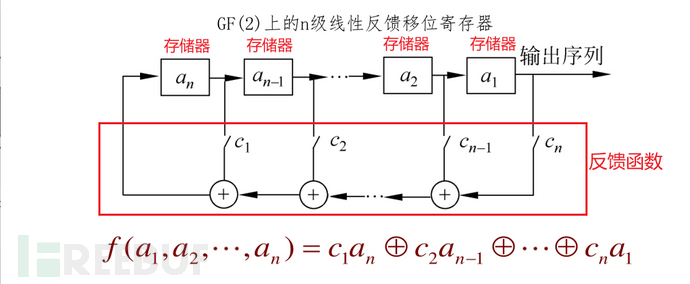
LFSR的输出序列{ $a_n$ }满足:
$f(a_1,a_2,...,a_n) = c_1a_n⊕c_2a_{n-1}⊕...⊕c_na_1$
$a{n+1} = c_1a_n⊕c_2a{n-1}⊕...⊕c_na_1$
$a{n+2} = c_1a{n+1}⊕c_2a_n⊕...⊕c_na_2$
.....
$a{n+i} = c_1a{n+i-1}⊕c_2a_{n+i-2}⊕...⊕c_na_i$(i = 1,2,3,...)
举例:
下面是一个5级的线性反馈移位寄存器,其初始状态为$(a_1,a_2,...,a_n)= (1,0,0,1,1)$
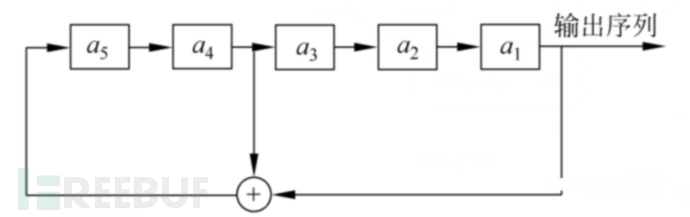
反馈函数为:$a{5+i} = a{3+i}⊕a_i$,(i = 1,2,...)可以得到输出序列为:
1001101001000010101110110001111 100110…
周期为31。
对于 n 级线性反馈移位寄存器,最长周期为$2^n-1$(排除全零)。达到最长周期的序列一般称为 m 序列
本文涉及相关实验:CTFCrypto练习之替换密码(本实验主要介绍了CTFCrypto练习之替换密码,通过本实验的学习,你能够了解CTF竞赛中的密码学题型,掌握凯撒密码破解方法,学会基于频率的替换密码破解方法。)
Part(1) 2018 强网杯 Streamgame1
考点:已知反馈函数,输出序列,求逆推出初始状态
题目:
from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
# 作用:判断字符串是否以指定字符 开头或结尾
assert len(flag)==25
def lfsr(R,mask):
output = (R << 1) & 0xffffff #将R向左移动1位,bin(0xffffff)='0b111111111111111111111111'
i=(R&mask)&0xffffff #按位与运算符&:参与运算的两个值,如果两个相应位都为1,则该位的结果为1,否则为0
lastbit=0
while i!=0:
lastbit^=(i&1) #按位异或运算,得到输出序列
i=i>>1
output^=lastbit #将输出值写入 output的后面
return (output,lastbit)
R=int(flag[5:-1],2) #flag为二进制数据
mask = 0b1010011000100011100
f=open("key","ab") #以二进制追加模式打开
for i in range(12):
tmp=0
for j in range(8):
(R,out)=lfsr(R,mask)
tmp=(tmp << 1)^out
f.write(chr(tmp)) #将lfsr输出的序列每8个二进制为一组,转化为字符,共12组
f.close()
考点:
def lfsr(R,mask):
output = (R << 1) & 0xffffff
i=(R&mask)&0xffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1 # R和mask进行异或操作,得到输出序列值
output^=lastbit #将输出值设置为output的最后一位
return (output,lastbit)
题目已知条件为 flag长度为19bits,mask长度也为19bits.
由LFSR的输出序列{ $a_n$ }满足的条件:
$a{n+i} = c_1a{n+i-1}⊕c_2a_{n+i-2}⊕...⊕c_na_i$(i = 1,2,3,...)
可知,输出值$a{n+i}$的结果与c的值相关,即题目中的mask。只有当c的值为1时,$c_1a{n+i-1},...,c_na_i$的值才可能为1
题目中mask中只有第(3,4,5,9,13,14,17,19)位为1,其余都是0(mask这里右边才是第一位,从右往左增大)
现在我们的目的就是为了求出前19位seed的值,而我们已知了seed后面输出序列的值(题目中给的附件key.txt)。那么我们逆推就能得到seed的值了。lfsr(R,mask)函数执行的是19bits的值。那么我们获取到输出序列前19bits值,即:
key = 0101010100111000111
现在需要计算$a{19}$的值,假设我们将 R = $a{19}010101010011100011$,进行lfsr(R,mask)运算,那么我们将得到输出值为 key[-1]=1。
因为mask中只有第(3,4,5,9,13,14,17,19)位为1,所以线性反馈函数只取这几位对应的a值
1=$a_{19}$^(R[-3])^(R[-4])^(R[-5])^(R[-9])^(R[-13])^(R[-14])^(R[-17])
得1=$a{19}$^0,得到$a{19}$=1
同理:R = $a{18}a{19}01010101001110001$ 的输出值为 key[-2]=1,求得$a_{18}$=1
第一种方法
#python3
from Crypto.Util.number import*
f = open('key.txt','rb').read()
r = bytes_to_long(f)
bin_out = bin(r)[2:].zfill(12*8)
R = bin_out[:19] #获取输出序列中与掩码msk长度相同的值
print(R)
mask = '1010011000100011100' #顺序 c_n,c_n-1,。。。,c_1
key = '0101010100111000111'
R = ''
for i in range(19):
output = 'x'+key[:18]
out = int(key[-1])^int(output[-3])^int(output[-4])^int(output[-5])^int(output[-9])^int(output[-13])^int(output[-14])^int(output[-17])
R += str(out)
key = str(out)+key[:18]
print('flag{'+R[::-1]+'}')
第二种方法
seed值只可能是0和1构成,所以猜就行了。
from Crypto.Util.number import*
import os,sys
os.chdir(sys.path[0])
f = open('key.txt','rb').read()
c = bytes_to_long(f)
bin_out = bin(c)[2:].zfill(12*8) #将key文本内容转换为 2 进制数,每个字节占 8 位
R = bin_out[0:19] #取输出序列的前19位
mask = 0b1010011000100011100
def lfsr(R,mask):
output = (R << 1) & 0xffffffff
i=(R&mask)&0xffffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
output^=lastbit
return (output,lastbit)
#根据生成规则,初始状态最后一位拼接输出序列
#我们可以猜测seed的第19位(0或1),如果seed19+R[:18]输出值等于R[:19],那么就可以确定seed值了
def decry():
cur = bin_out[0:19] #前19位 2 进制数
res = ''
for i in range(19):
if lfsr(int('0'+cur[0:18],2),mask)[0] == int(cur,2):
res += '0'
cur = '0'+cur[0:18]
else:
res += '1'
cur = '1' + cur[0:18]
return int(res[::-1],2)
r = decry()
print(bin(r))
第三种方法
import os,sys
os.chdir(sys.path[0])
from Crypto.Util.number import *
key = '0101010100111000111'
mask = 0b1010011000100011100
R = ""
index = 0
key = key[18] + key[:19]
while index < 19:
tmp = 0
for i in range(19):
if mask >> i & 1:
tmp ^= int(key[18 - i])
R += str(tmp)
index += 1
key = key[18] + str(tmp) + key[1:18]
print (R[::-1])
Part(1) 2018 强网杯 Streamgame2
考点:已知反馈函数,输出序列,求逆推出初始状态
题目
from flag import flag
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==27
def lfsr(R,mask):
output = (R << 1) & 0xffffff
i=(R&mask)&0xffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
output^=lastbit
return (output,lastbit)
R=int(flag[5:-1],2)
mask=0x100002
f=open("key","ab")
for i in range(12):
tmp=0
for j in range(8):
(R,out)=lfsr(R,mask)
tmp=(tmp << 1)^out
f.write(chr(tmp))
f.close()
解法与 2018 强网杯 Streamgame1不能说是毫不相干,简直是一m0一样
from Crypto.Util.number import*
bin_out = open('key.txt','rb').read()
key = bin(bytes_to_long(bin_out))[2:]
# print(key[0:21])
# print(bin(int('0x100002',16)))
key = '101100101110100100001'
mask= '100000000000000000010'
R = ''
for i in range(21):
output = '?' + key[:20]
ans = int(key[-1]) ^ int(output[-2])
R += str(ans)
key = str(ans) + key[:20]
print(R[::-1])
Part(3) [CISCN2018]oldstreamgame
考点:和前面的题目一样都是给出输出序列和反馈函数,求seed(初始状态)
题目:
flag = "flag{xxxxxxxxxxxxxxxx}"
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==14
def lfsr(R,mask):
output = (R << 1) & 0xffffffff
i=(R&mask)&0xffffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
output^=lastbit
return (output,lastbit)
R=int(flag[5:-1],16)
mask = 0b10100100000010000000100010010100
f=open("key","w")
for i in range(100):
tmp=0
for j in range(8):
(R,out)=lfsr(R,mask)
tmp=(tmp << 1)^out
f.write(chr(tmp))
f.close()
exp
#python3
import os,sys
os.chdir(sys.path[0])
from Crypto.Util.number import*
f = open('key.txt','rb').read()
key = bytes_to_long(f)
bin_out = bin(key)[2:].zfill(100*8)
# print(bin_out[:32]) #前32位就是key
key = '00100000111111011110111011111000'
mask = '10100100000010000000100010010100'
R = ''
for i in range(32):
output = 'x' + key[:31]
ans = int(key[-1]) ^ int(output[-3]) ^ int(output[-5]) ^ int(output[-8]) ^ int(output[-12]) ^ int(output[-20]) ^ int(output[-27]) ^ int(output[-30])
R += str(ans)
key = str(ans) + key[:31]
R = str(hex(int(R[::-1],2))[2:])
flag = "flag{" + R + "}"
print(flag)
Part(4) [De1CTF2019]Babylfsr
考点:B-M 算法
题目给了度为256的lfsr,和输出长度为504的输出序列,并提示了FLAG的特征。
在CTFWiki中有介绍道 B-M 算法:如果我们知道了长度为 2n 的输出序列,那么就可以通过构造矩阵来求出 mask,时间复杂度:$O(n^2)$ 次比特操作,空间复杂度:$O(n)$ 比特。
题目:
import hashlib
from secret import KEY,FLAG,MASK
assert(FLAG=="de1ctf{"+hashlib.sha256(hex(KEY)[2:].rstrip('L')).hexdigest()+"}")
assert(FLAG[7:11]=='1224')
LENGTH = 256
assert(KEY.bit_length()==LENGTH)
assert(MASK.bit_length()==LENGTH)
def pad(m):
pad_length = 8 - len(m)
return pad_length*'0'+m
class lfsr():
def __init__(self, init, mask, length):
self.init = init
self.mask = mask
self.lengthmask = 2**(length+1)-1
def next(self):
nextdata = (self.init << 1) & self.lengthmask
i = self.init & self.mask & self.lengthmask
output = 0
while i != 0:
output ^= (i & 1)
i = i >> 1
nextdata ^= output
self.init = nextdata
return output
if __name__=="__main__":
l = lfsr(KEY,MASK,LENGTH)
r = ''
for i in range(63):
b = 0
for j in range(8):
b = (b<<1)+l.next()
r += pad(bin(b)[2:])
with open('output','w') as f:
f.write(r)
这题中输出序列只给出了504个值,根据 B-M 算法,我们需要确定512个值 (即长度为2n的序列,n为lfsr的度,这里是256) 才能求出 mask ,所以我们可以爆破序列后面缺失的 8 位,可以得到 256 种 mask 可能值,用这 256 个 mask 恢复出 256 个key 值,再用限制条件筛选出 flag.
#sage
import hashlib
key = '001010010111101000001101101111010000001111011001101111011000100001100011111000010001100101110110011000001100111010111110000000111011000110111110001110111000010100110010011111100011010111101101101001110000010111011110010110010011101101010010100101011111011001111010000000001011000011000100000101111010001100000011010011010111001010010101101000110011001110111010000011010101111011110100011110011010000001100100101000010110100100100011001000101010001100000010000100111001110110101000000101011100000001100010'
#将二进制数据填充为8位
def pad(x):
pad_length = 8 - len(x)
return '0'*pad_length+x
# 获取 256个 key 可能值
def get_key(mask,key):
R = ""
index = 0
key = key[255] + key[:256]
while index < 256:
tmp = 0
for i in range(256):
if mask >> i & 1:
# tmp ^= int(key[255 - i])
tmp = (tmp+int(key[255-i]))%2
R = str(tmp) + R
index += 1
key = key[255] + str(tmp) + key[1:255]
return int(R,2)
# 将二进制流转化为十进制
def get_int(x):
m=''
for i in range(256):
m += str(x[i])
return (int(m,2))
# 获取到256个 mask 可能值,再调用 get_key()函数,获取到key值,将结果导入到 sm 中
sm = []
for pad_bit in range(2**8): #爆破rr中缺失的8位
r = key+pad(bin(pad_bit)[2:])
index = 0
a = []
for i in range(len(r)):
a.append(int(r[i])) #将 r 转换成列表a = [0,0,1,...,]格式
res = []
for i in range(256):
for j in range(256):
if a[i+j]==1:
res.append(1)
else:
res.append(0)
sn = []
for i in range(256):
if a[256+i]==1:
sn.append(1)
else:
sn.append(0)
MS = MatrixSpace(GF(2),256,256) #构造 256 * 256 的矩阵空间
MSS = MatrixSpace(GF(2),1,256) #构造 1 * 256 的矩阵空间
A = MS(res)
s = MSS(sn) #将 res 和 sn 的值导入矩阵空间中
try:
inv = A.inverse() # 求A 的逆矩阵
except ZeroDivisionError as e:
continue
mask = s*inv #构造矩阵求mask,B-M 算法
# print(mask[0]) #得到 256 个 mask 值(),type元组
# print(get_int(mask[0]))
# print(key_list)
# print(key[:256])
# print(hex(solve(get_int(mask[0]),key[:256])))
# break
sm.append(hex(get_key(get_int(mask[0]),key[:256])))
# 通过限制条件确定 最终 的flag值
for i in range(len(sm)):
FLAG = hashlib.sha256(sm[i][2:].encode()).hexdigest()
if FLAG[:4]=='1224':
print('flag{'+FLAG+'}')
output:
flag{1224473d5e349dbf2946353444d727d8fa91da3275ed3ac0dedeb7e6a9ad8619}
上面是我关于LFSR学习的一点总结,希望对大家有所帮助,后面会介绍关于LFSR更多的知识点.
如有侵权请联系:admin#unsafe.sh