FreeBuf.COM网络安全行业门户，每日发布专业的安全资讯、技术剖析。

长城杯 CTF 2025 - 核心题目复盘 Writeup

本次复盘涵盖了逆向工程、密码学、流量取证及二进制漏洞利用四个方向的核心题目。

Reverse: EzFlag

1. 题目概况

• 文件类型: 64-bit ELF C++ (Not Stripped)

• 运行环境: 本地运行提示GLIBCXX_3.4.32 not found，因此采用静态分析为主。

2. 静态分析与密码获取

通过strings命令快速定位关键字符串，发现程序中存在明文硬编码：

Bash

strings -n 4 EzFlag | grep -E "Enter password|flag\{|V3ry"

分析 main 函数逻辑（IDA/Ghidra）：

程序首先通过 getline 读取用户输入，并与 .rodata 段中的字符串进行对比：

• Check:input != "V3ryStr0ngp@ssw0rd"

• Result: 若不相等则退出，相等则进入 Flag 生成逻辑。

第一步密码:V3ryStr0ngp@ssw0rd

3. Flag 生成算法分析

程序在验证密码通过后，输出flag{，随后进入一个 32 次的循环。每次循环调用函数f(y)生成一个字符，并按8-5-5-5-9的格式插入连字符-。

核心函数 f(y) 逻辑：

这是一个典型的斐波那契数列变形。

• 初始化：$a=0, b=1$

• 循环 $y$ 次进行更新：$b_{new} = (a+b) \pmod{16}$

• 返回值：查表K[a]，其中K = "012ab9c3478d56ef"。

变量 y 的膨胀问题：

在主循环中，y 的更新公式为：

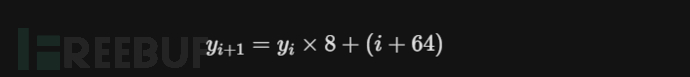
由于 $y$ 呈指数级增长，直接模拟计算 $F_y$ 会导致溢出或超时。

4. 算法优化与解密

观察到我们只需要 $F_y \pmod{16}$。根据 Pisano Period（皮萨诺周期）性质，斐波那契数列在模 $n$ 下是周期的。

• 对于 $n=16$，其 Pisano 周期为 24。

• 因此，我们只需维护 $y \pmod{24}$ 即可瞬间算出结果。

5. 解题脚本 (Python)

Python

K = "012ab9c3478d56ef"

# 1. 预计算 Fibonacci mod 16 的周期表 (周期=24)
fib_mod = []
a, b = 0, 1
for _ in range(24):
    fib_mod.append(a)
    a, b = b, (a + b) % 16

# 2. 模拟生成 Flag
y = 1 % 24  # 初始 y
flag_chars = []

for i in range(32):
    # 取斐波那契数对应的查表字符
    flag_chars.append(K[fib_mod[y]])
    
    # 格式化插入 '-'
    if i in (7, 12, 17, 22):
        flag_chars.append('-')
        
    # 更新 y (模 24 即可)
    y = (y * 8 + i + 64) % 24

print(f"flag{{{''.join(flag_chars)}}}")

Crypto: Inner/Outer RSA

1. 题目参数分析

题目给出了两层 RSA 结构，这是一种非常特殊的 Multi-prime RSA 变体：

2. 漏洞原理：Pollard's p-1 变体攻击

标准的 Pollard's $p-1$ 攻击依赖于 $p-1$ 仅包含小因子。本题中 $p-1 = k_p \cdot p_1$，其中 $p_1$ 是大素数（512-bit），导致标准攻击失效。

攻击向量：

虽然 $p_1$ 未知，但我们知道 $n_1$ 是 $p_1$ 的倍数。

我们可以构造特殊的指数 $E$ 来利用费马小定理：

免责声明

1.一般免责声明：本文所提供的技术信息仅供参考，不构成任何专业建议。读者应根据自身情况谨慎使用且应遵守《中华人民共和国网络安全法》，作者及发布平台不对因使用本文信息而导致的任何直接或间接责任或损失负责。

2. 适用性声明：文中技术内容可能不适用于所有情况或系统，在实际应用前请充分测试和评估。若因使用不当造成的任何问题，相关方不承担责任。

3. 更新声明：技术发展迅速，文章内容可能存在滞后性。读者需自行判断信息的时效性，因依据过时内容产生的后果，作者及发布平台不承担责任。

本文为 独立观点，未经授权禁止转载。
如需授权、对文章有疑问或需删除稿件，请联系 FreeBuf 客服小蜜蜂（微信：freebee1024）