0.前言

这次鹏城杯真的是燃尽了，能不能进线下就看命了

1.cry

1.1 babyrsa

一道典型的RSA 密钥恢复题目，具体来说，它是利用高精度浮点数泄露来还原私钥参数的题目 题目给出了一个名为 leak 的变量，其计算公式为

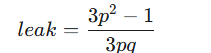
这道题之所以会发生泄露，核心原因在于：题目给出的十进制小数精度远大于还原分数所需的信息量

简单来说，是因为给的小数点后的位数太多了，多到足以精确地反向推算出原本的分子和分母，举个例子来说:

低精度假设原本分数是 1/3，但我只告诉你 0.3

你无法确定是 1/3，还是3/10，这就很安全，因为精度丢失了。

但是高精度：假设原本分数是 1/3，我告诉你 0.33333333...给了你足够的位数，你会发现只有 1/3

这个简单的分数能完美匹配这一长串数字，而不是 3333/10000这种复杂的数字

这道题，分母只需要约617 位就能表示，题目却给了1024 位的信息

1024 > 617，这多出来的 400 多位精度，保证了我们可以毫无歧义地将这个小数转回唯一的那个分数

exp.py

import decimal
from Crypto.Util.number import long_to_bytes
​
# --- 题目数据 ---
leak_str = "1.396995694831414203476063690838730308815841662737318558906107823553922718340982125801595368449608188770051881765292978548960520326036779130167518285237817101541807766017642530065080930654694948943506714268685400709580398894902693407016988670394423892586264077247263710263220932577837642377245651448838665854362532801659965471421937839336237670710012298796758992931116659292915200628873553198226185187089027680973673618973869464164460226697625936493428822424637497370197316811245879504779934098600596822159243994319583651080005054538419168988020562590543262648544970376255020489363894055887067948343768399654357738592577280906555896933717091837896978973488220368081406433117367524537063718421897982643644320078600517763936883820416362057895941185749296170109172249907094176821124345672294602380784325702476105763209165109703429326132417850746805701054961710623030742187505484821961670922386999933202645522248608323217011522889282323071281405301772218220381951540118124201599862330377374571641729649420917168701463539034702411"
d = 16306054997613721520756151430779642117683661431522665108784419231044104572118893098180652730976905729602478591047033305251624752030036736271198006715513694904231940253554804069707679445942892410812386221633728427239116007373836662495075237456279818311659331982404534490546781763464409713789636372508503902598331950861474527128323735250673137355260113147338636761737748874105625008482750923429512271416511835596944209137554445130949731646669691366003832655082535985891463876904334888009751956386994969339847254470145428608062575606120441725590059524749595027078238962391188809496875025237129899849787699468205026040721
c = 7908369000608075306226552240713890041649799894903074579356627811865842237315201153498579205223600526520994811661608630888045462921547166872107507948062717836952855804806976414887413729060431265217539895710936669089248515746191716161194996469977577048602427553584286064475300979649416171469313168995504717602670924606819204605601860560767900702512753735554900344201907921239415885901489708576066483012272256175573658509614344875077232108364134161997767814675830320630271209201503987787921279932886374846298269125068817280777403718279754392091441050281244934594776307137448975055247018414699621410668188864774860026941
​
# --- 求解脚本 ---
# 设置足够的精度 (大于leak的位数)
decimal.getcontext().prec = 5000 
L = decimal.Decimal(leak_str)
​
# 尝试常见的 e 值
e_list = [65537, 3, 5, 17, 257]
​
print("开始寻找 flag ...")
​
for e in e_list:
# k 的范围通常在 1 到 e 之间
for k in range(1, e):
# 检查 k 是否能整除 e*d - 1
if (e * d - 1) % k == 0:
phi = (e * d - 1) // k
# 使用一元二次方程求 q 的近似值: L*q^2 - (L+1)*q + (1-phi) = 0
# 判别式 delta = (L+1)^2 - 4*L*(1-phi)
#           = (L+1)^2 + 4*L*(phi-1)
term1 = (L + 1) ** 2
term2 = 4 * L * (decimal.Decimal(phi) - 1)
delta = term1 + term2
if delta < 0:
continue
# 求解正根 (q 是大素数，取正号)
sqrt_delta = delta.sqrt()
q_approx = (L + 1 + sqrt_delta) / (2 * L)
# 转为整数并搜索附近的整数
q_int = int(q_approx)
# 搜索范围可以很小，因为 leak 精度极高
for q_cand in range(q_int - 2, q_int + 3):
if q_cand < 2: continue
# 验证: (q-1) 必须整除 phi
if phi % (q_cand - 1) == 0:
p_cand = phi // (q_cand - 1) + 1
n = p_cand * q_cand
try:
# 尝试解密
m_int = pow(c, d, n)
m_bytes = long_to_bytes(m_int)
# 检查 flag 特征
if b'ISCTF' in m_bytes or b'flag' in m_bytes:
print(f"\n[+] 成功找到 Flag (e={e}, k={k})")
print(f"[+] Flag: {m_bytes.decode()}")
exit()
except Exception:
pass
print("[-] 未找到 Flag，请检查输入数据或参数。")

1.2 peco

这是一道复合型密码学题目，融合了多种数论和格密码攻击技术

主要类型可以归纳为：RSA 密钥恢复 + 不定方程求解 + 格格归约

基本思路就是

1.解不定方程→获得 x,y

2.Hensel Lifting亨泽尔引理 + Coppersmith →分解 n→解密得到 m

3.构造 Lattice 使用 LL→求解 f0,f1→拼接得到 Flag

exp.py

import sys
​
# 手动实现 long_to_bytes
def long_to_bytes(val, endianness='big'):
val = int(val)
if val == 0: return b'\x00'
width = (val.bit_length() + 7) // 8
return val.to_bytes(width, byteorder=endianness)
​
# --- 题目数据 ---
n = 18443962106578943927922829208562388331564422618353954662348987125496135728205879853444693999188714508145409575298801277623433658530589571956301880815632542860363148763704636874275223979061507756787642735086825973011622866458454405794279633717255674221895468734500735123736684346340314680683830866884050311047424068122453972745273167956795195575475691048908906061023817574695902603984554911326264947716547564759877947888574515784489778380086664649338093680740990860192640619047071160362288611331225632270531304525264824445326394068892806774552310748255977040249822464839809344521107040968321810533993659358229305320413
c = 8176283809770578639445916571748890916863681496488338436815389781344271720445865752568007651231910205530735296305471880971422173915403956857863330698931559658909826642456860761540607878553228782799635976463090037022164739976302533892173751687781100980039065722082091714141141136171701360981540040678479802206949078162548124224838019262997441233919136963696523351831737708850863538007579105976954619102728135600542584651031405327214877358323388674864043740117718200022790892542634633918493245432384562983429810936975869853596007429259749282607844407676244954057886824475948603911174707176467261179324130051317766768127
gift1_A = 1293023064232431070902426583269468463
gift1_B = 105279230912868770223946474836383391725923
gift2 = 26161714402997656593966327522661504448812191236385246127313450633226841096347099194721417620572738092514050785292503472019045698167235604357096118735431692892202119807587271344465029467089266358735895706496467947787464475365718387614
e = 65537
​
# --- 全局变量存储结果 ---
val_x = None
val_y = None
p_found = None
q_found = None
m_dec = None
​
print("=== 步骤 1: 求解佩尔方程 x, y ===")
# 你的日志显示这步已经成功了，我保留代码以确保完整性
g = gcd(gift1_A, gift1_B)
A_prime = gift1_A // g
B_prime = gift1_B // g
D = A_prime * B_prime
K.<sqrtD> = QuadraticField(D)
​
try:
unit = K.units()[0]
# 转换为整数单元
curr = unit
u, v = 0, 0
# 尝试几次幂来消除分母 (通常 1 或 2 次即可)
for _ in range(6):
try:
u = ZZ(curr[0])
v = ZZ(curr[1])
break
except TypeError:
curr = curr * unit
else:
print("[-] 无法找到整数解，跳过 x,y 求解 (如果之前已算出可手动填入)")
if u**2 - D*v**2 == -1:
u, v = u**2 + D*v**2, 2*u*v
val_x = u
val_y = A_prime * v
print(f"[+] 找到 x: {str(val_x)[:30]}...")
print(f"[+] 找到 y: {str(val_y)[:30]}...")
​
except Exception as e:
print(f"[-] Pell 求解出错: {e}")
​
if val_x is not None:
print("\n=== 步骤 2: Hensel Lifting 恢复 p 低位 ===")
p_cands = [1]
mod_limit_bits = 777
for k in range(1, mod_limit_bits):
next_mod = 1 << (k + 1)
new_cands = []
for val in p_cands:
for bit in [0, 1]:
cand = val | (bit << k)
try:
# 验证 p^7 + (n/p)^13 == gift2
inv_p = inverse_mod(cand, next_mod)
q_val = (n * inv_p) % next_mod
lhs = (pow(cand, 7, next_mod) + pow(q_val, 13, next_mod)) % next_mod
if lhs == (gift2 % next_mod):
new_cands.append(cand)
except: pass
p_cands = new_cands
if not p_cands:
print(f"[-] Lifting 在第 {k} 位中断")
break
print(f"[+] Lifting 完成，候选数量: {len(p_cands)}")
print("\n=== 步骤 3: Coppersmith 恢复完整 p ===")
P_poly.<x_poly> = PolynomialRing(Zmod(n))
# 遍历所有候选 p0
for idx, p0 in enumerate(p_cands):
print(f"[*] 正在尝试候选 {idx+1}/{len(p_cands)} ...")
# 构造多项式 f(x) = p0 + x * 2^777
f = p0 + x_poly * (1 << mod_limit_bits)
f = f.monic()
# 【关键优化】
# 未知位数 = 1024 - 777 = 247 bits
# 设置 X 为 2^250 (略大于247)，beta 为 0.4
# 只要 X < N^(beta^2) 即可。N^0.16 ≈ 320 bits > 250 bits，条件满足且计算快。
try:
roots = f.small_roots(X=2**250, beta=0.4)
if roots:
p_high = int(roots[0])
p_check = p0 + p_high * (1 << mod_limit_bits)
if n % p_check == 0:
p_found = p_check
q_found = n // p_check
print(f"[+] 成功分解 n !")
break
except Exception as e:
print(f"[-] Coppersmith 错误: {e}")
continue
​
if p_found:
print("\n=== 步骤 4: RSA 解密 m ===")
phi = (p_found - 1) * (q_found - 1)
d_rsa = inverse_mod(e, phi)
m_dec = pow(c, d_rsa, n)
print(f"[+] m = {m_dec}")
print("\n=== 步骤 5: LLL 求解 Flag ===")
# 构造格矩阵
M = Matrix(ZZ, [
[1, 0, val_x],
[0, 1, val_y],
[0, 0, m_dec]
])
print("[*] 正在执行 LLL ...")
L = M.LLL()
print("[*] 搜索结果向量 ...")
for row in L:
f0_cand = abs(row[0])
f1_cand = abs(row[1])
r_cand = abs(row[2])
# 题目约束 r < 2^99，这里放宽一点检查
if r_cand < 2**110:
s0 = long_to_bytes(int(f0_cand))
s1 = long_to_bytes(int(f1_cand))
# 检查所有可能的拼接组合
cands = [s0 + s1, s1 + s0]
for flag_bytes in cands:
if b"flag{" in flag_bytes or b"ISCTF" in flag_bytes:
print(f"\n[SUCCESS] Flag: {flag_bytes.decode(errors='ignore')}")
sys.exit(0)
print("[-] 未能自动识别 Flag，请手动检查以下向量:")
for row in L[:3]:
print(row)
else:
print("[-] 未能分解 n")

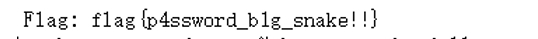
2.misc

2.1 blue

给了一张图片，但是啥都看不清

提取blue部分的像素值看看结果：

from PIL import Image
​
img = Image.open('blue.png')
width, height = img.size
​
s = []
for i in range(width):
for j in range(1):
tmp = img.getpixel((i,j))
s.append(tmp[2])
​
print(bytes(s).hex())

发现取出每个字节的高8位，可以组成zip（开头504b0304），处理

from PIL import Image
from tqdm import *
​
img = Image.open('blue.png')
width, height = img.size
​
s = ''
for i in trange(height):
for j in range(width):
tmp = img.getpixel((j,i))
#print(hex(tmp[2]>>4)[2:])
s += hex(tmp[2]>>4)[2:]
​
open('oo.zip','wb').write(bytes.fromhex(s))

得到zip，加密，里面有xor.png 试试看用明文攻击

bkcrack.exe -C oo.zip -c xor.png -x 0 89504e470d0a1a0a0000000d4948445200

得到key 68cc45ab 864060ce ac958caa

.\bkcrack.exe -C oo.zip -c xor.png -k 68cc45ab 864060ce ac958caa -d xor.png

得到 xor.png，末尾有另一个png，提取出来，根据名字xor，将两幅图异或得到xor1.png:

from PIL import Image
import numpy as np
​
# 打开图片
img1 = Image.open("xor.png")
img2 = Image.open("Untitled1.png")
​
# 确保模式和尺寸一致
assert img1.size == img2.size
assert img1.mode == img2.mode
​
# 转为 numpy 数组
arr1 = np.array(img1)
arr2 = np.array(img2)
​
# 像素逐位 XOR
xor_arr = arr1 ^ arr2
​
# 转回 Image 并保存
xor_img = Image.fromarray(xor_arr)
xor_img.save("xor1.png")

得到的xor1.png与xor.png类似，盲水印解，解完就可以得到flag了

2.2 Hidden

给了一个.bmp格式的图片，zsteg查看lsb：

zsteg -a treasure.bmp

再尝试steghide隐写，密码PixelWhisper：

steghide extract -sf treasure.bmp

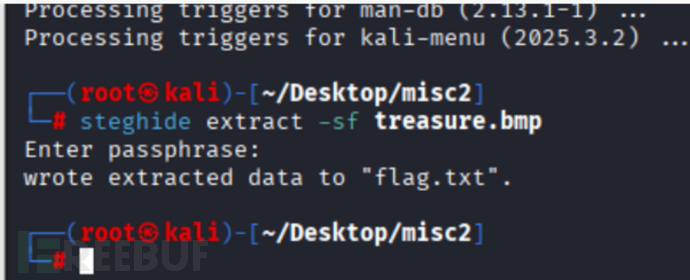
去看看flag.txt

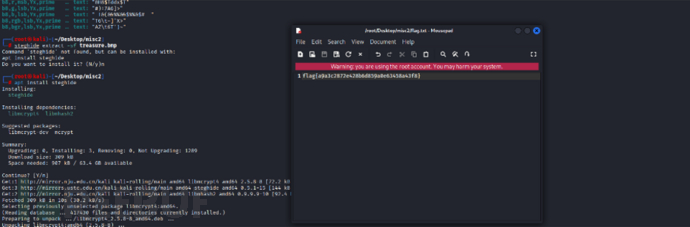
flag{a9a3c2872e428b6d859a0e63458a43f8}

2.3 the_rogue_beacon

一个流量包，用wirehark打开

题目说要找到其峰值，这么多流量帧看得我眼睛疼

【----帮助网安学习，以下所有学习资料加v~x：YJ-2021-1，备注“freebuf”获取！】

① 网安学习成长路径思维导图
② 60+网安经典常用工具包
③ 100+SRC漏洞分析报告
④ 150+网安攻防实战技术电子书
⑤ 最权威CISSP 认证考试指南+题库
⑥ 超1800页CTF实战技巧手册
⑦ 最新网安大厂面试题合集（含答案）
⑧ APP客户端安全检测指南（安卓+IOS）

观察数据包，发现主要存在两个疑似传输数值的 ID：

· ID 0x039：数据跳变剧烈，无规律，判断为干扰信号

· ID 0x244：数值呈现平滑的加速趋势，符合物理运动规律，锁定为真实车速信号

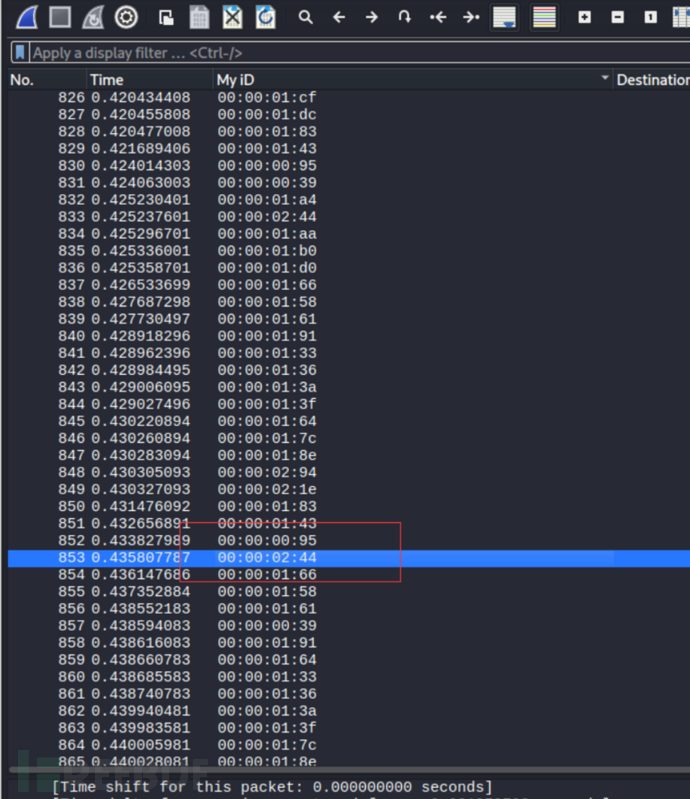
由于题目文件中的 CAN-ID 采用大端存储，直接解析 ID 0x244 对应的 Hex 为 00 00 02 44。

在过滤器栏输入以下指令，仅显示真实车速数据，输入 frame[0:4] contains 00:00:02:44 ，只显示真实车速数据包

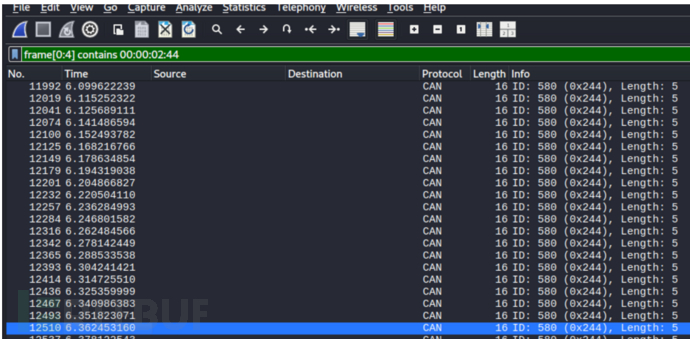
搜索到12149帧，此时的数据是35e4

上一行的数据是35d1，比35e4小

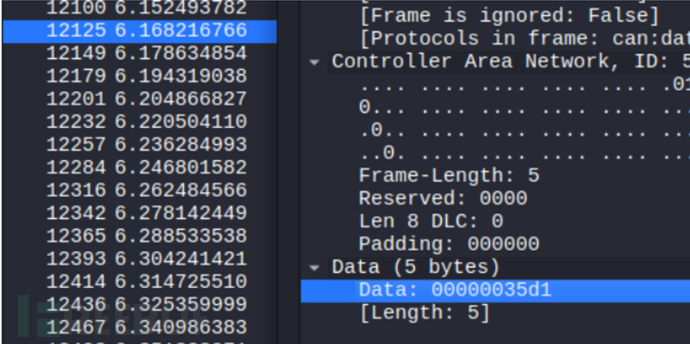
下一行的数据也是35d1，比35e4小，说明12149号帧就是峰值

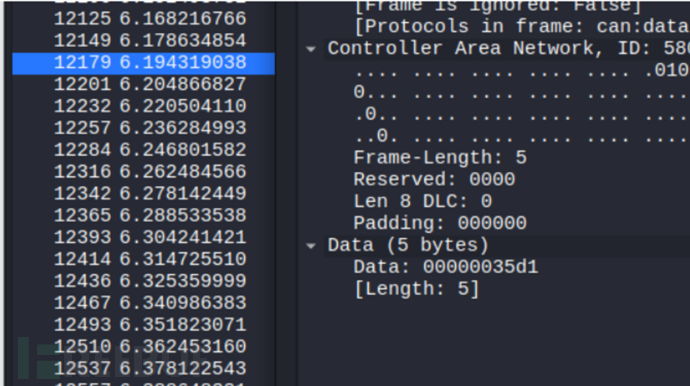
而题目要求是sha-256加密，那直接拿12149去哈希就是flag了

flag{9db878fd06dd7587a91c0fb600e0e9f7c3ea310e75f36253ef57ac2d92dd8c29}

2.4 SMB

这道题其实是流量分析和逆向的结合

使用 Wireshark 打开提供的流量包文件，观察流量包中的协议分布

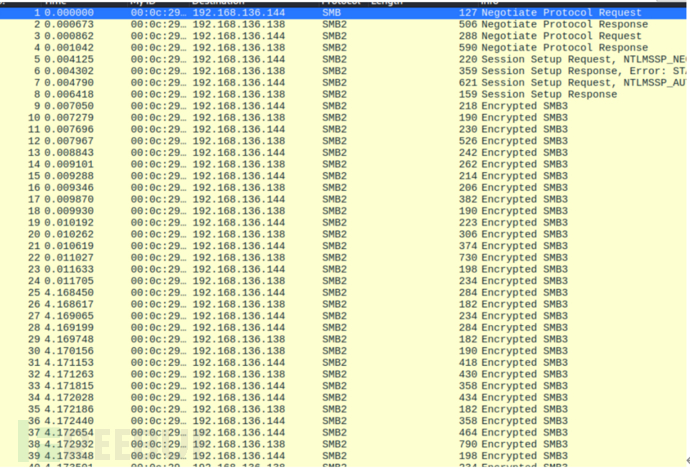
在流量包中发现大量 SMB 协议流量，SMB 是 Windows 系统中用于文件共享的协议，流量中可能包含传输的文件

发现一个名为letter.exe的可执行文件将该文件保存到本地

然后就是逆向的部分了，ida启动

这居然还是rust语言的

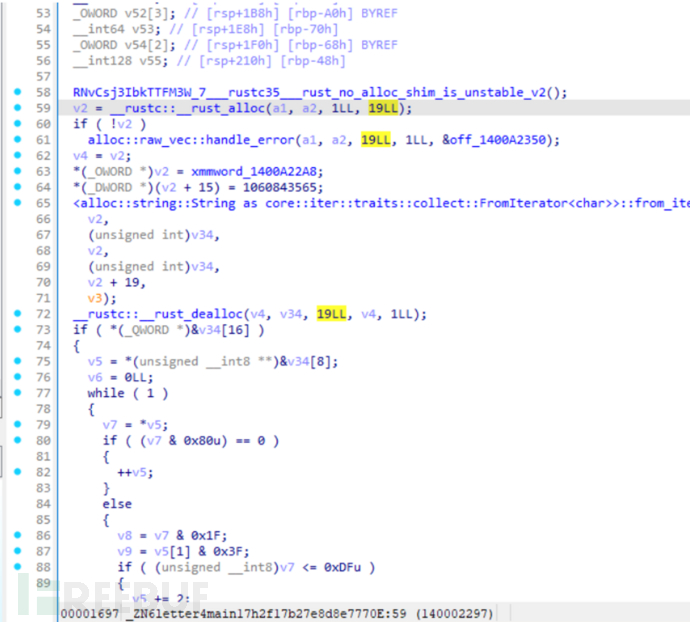
真正的主函数是这个letter::main，不是main

v2 = __rustc::__rust_alloc(a1, a2, 1LL, 19LL); //这里应该是分配内存
​
//从地址 0x1400A22A8 复制 19 字节数据
​
*(_OWORD *)v2 = xmmword_1400A22A8;
​
*(_DWORD *)(v2 + 15) = 1060843565;

在 IDA 中定位到地址0x1400A22A8使用 Hex View 查看该地址的数据

刚好是19个字符串，怀疑这里就是flag，数据中包含可打印字符和不可打印字符，怀疑使用了简单的加密算法

编写 Python 脚本尝试常见的 XOR 密钥，当 XOR 密钥为0x42时，成功解密出 flag

2.5 zipcracker

给了三个东西

do u know it是一个grc文件，将 I/Q 的实部、虚部分别写入文件

something in it.jpg末尾有个zip，提取出来，可以得到 flag1.txt和 flag2.txt，分别是 I/Q 的实部、虚部

重构复数 IQ，然后NBFM解调，再低通+降采样到音频速率，保存为wav文件：

import numpy as np
from scipy.signal import decimate
from scipy.io.wavfile import write
​
I = np.fromfile("Untitled1/flag1.txt", dtype=np.float32)
Q = np.fromfile("Untitled1/flag2.txt", dtype=np.float32)
iq = I + 1j * Q
​
phase = np.unwrap(np.angle(iq))
fm = np.diff(phase)
​
audio = decimate(fm, 4)
print(audio)
​
write("out.wav", 48000, audio / np.max(np.abs(audio)))

获得一段音频，一听就知道是摩斯密码

提取一下 .---- .---- ....- ..... .---- ....- ...-- ..... ----- ..--- ...-- ....- .---- .---- ....- ..... .---- ....-

翻译过来就是114514350234114514

解压flag.zip，其中flag.txt是头尾已知的部分明文，flag.zip是包含flag.txt的加密压缩包

明文攻击

bkcrack.exe -C flag.zip -c flag.txt -x 0 666c61677b593075 -x 25 2121217d

得到三个key 33b19021 93c4a78d 9ceed931

拿ARCHPR去跑，就可以得到flag

3.re

3.1 more_more_flower

Windows 32-bit PE 可执行文件Console 程序

给的flagSHA256.txt：给了一个 flag 的 SHA256，用来最后校验结果

flagSHA256.txt内容类似：

flag SHA256 Encrypted:3dbe89f66cb189f9cac1fb5ec23fac941df69119792aad4b6d61d63b98ddb527

IDA里面跟flag有关的就是这个函数

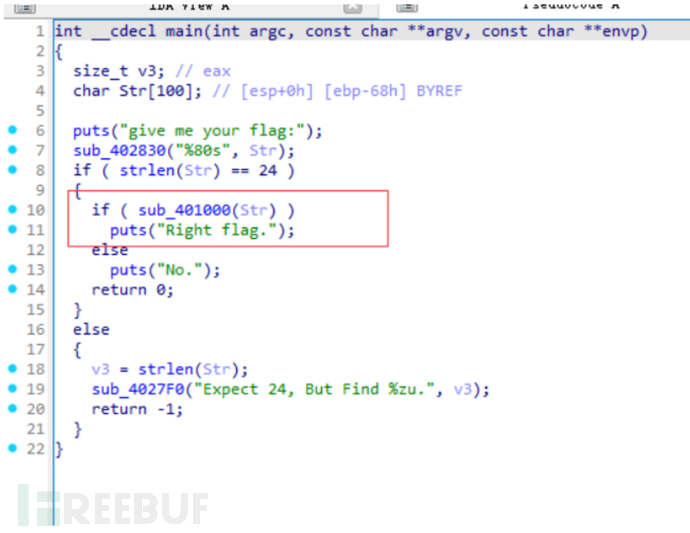
sub_401000这个函数很长，大概就是 全局变量每轮从.data里取 opcode 还有dispatch jump table，opcode -> handler 地址

还有全局寄存器R0C、R10、R14、R18、R28…

最后还在在.data里开了一段空间 + SP 指针，就是用来验证flag

输入长度固定为 0x18（24）字节，处理时按 dword对齐读取，因此总共会跑6 个 block

每次取 4 字节时，先按高字节在前拼成 32-bit 值：

-v = (b0<<24) + (b1<<16) + (b2<<8) + b3

完成该 block 的运算后，结果不会按原顺序写回，而是把 dword 拆成 小端序的 4 个字节压入 VM 栈

并没有单独的 loop 变量，而是把计数放在 栈底第 0 字节 启动阶段先PUSH 0x06，每处理完一组就对STACK[0]做-1，再用JNZ STACK[0]来决定要不要继续下一组

每个 4 字节 block 内部会进入一个固定轮数的 ARX 更新流程，风格接近 TEA 那类“sum 逐轮叠加 delta”的写法

-sum初始清零（VM 里对应 R18）

- 轮数硬编码为0x1e（即 30）

每轮的顺序是先累加：

-sum += delta

随后再更新数据本体v：

-v += ((v<<5) ^ sum ^ (v>>4))

delta不是直接出现的立即数，而是由字节码“拼装”出来：每轮都会 push 四个字节56 11 25 23，再 POP 成 dword，因此得到常量：

-delta = 0x23251156

6 组数据全部处理完后，VM 栈里会累计得到 24 个变换后的输出字节；随后 bytecode 进入固定 24 次的校验循环，每次都从栈顶 POP 1 字节并与.data段中的常量数组DATA[i]通过SUB+JNZ逐一比对，一旦不相等就直接走失败分支RET 0。由于校验是“从栈顶往下弹”，实际比较顺序与生成顺序相反，因此整体等价于检查DATA == reverse(out)。从.data中提取的 24 字节常量为21 7a 01 1c 33 d3 3e f7 03 78 25 5e 2f b8 8b 3b 93 84 ae 5b de a5 d6 e9，将其反序后再按每 4 字节以小端拼回 6 个 32-bit 密文块，分别是0xDEA5D6E9, 0x9384AE5B, 0x2FB88B3B, 0x0378255E, 0x33D33EF7, 0x217A011C，于是问题就转化为：在已知这 6 个 32-bit 输出的情况下，求对应的 6 个由 4 个可打印字符组成的 32-bit 输入

用python会跑得很慢，所以直接改为用C++好了

#pragma GCC optimize("O3,unroll-loops")
#include <iostream>
#include <vector>
#include <string>
#include <iomanip>
#include <cstdint>
#include <array>
​
// 配置常量
const uint32_t CFG_DELTA = 0x23251156;
const int CFG_ROUNDS = 30;
​
// 待解密的密文块 (从 .data 提取)
const std::vector<uint32_t> TARGETS = {
0xDEA5D6E9, 0x9384AE5B, 0x2FB88B3B, 
0x0378255E, 0x33D33EF7, 0x217A011C
};
​
// 预计算 acc 表，避免重复计算
uint32_t ACC_TABLE[CFG_ROUNDS];
​
void precompute_acc() {
uint32_t acc = 0;
uint32_t delta = CFG_DELTA;
for(int i = 0; i < CFG_ROUNDS; i++) {
acc += delta;
ACC_TABLE[i] = acc;
}
}
​
// 核心加密函数 (内联以提速)
inline uint32_t encrypt_core(uint32_t v) {
for (int i = 0; i < CFG_ROUNDS; i++) {
// v = v + ((v << 5) ^ acc ^ (v >> 4))
v += ((v << 5) ^ ACC_TABLE[i] ^ (v >> 4));
}
return v;
}
​
// 辅助：将整数转为字符串（自动处理字节序）
std::string u32_to_str(uint32_t val, bool little_endian) {
std::string s(4, ' ');
if (little_endian) {
s[0] = (val >> 0) & 0xFF;
s[1] = (val >> 8) & 0xFF;
s[2] = (val >> 16) & 0xFF;
s[3] = (val >> 24) & 0xFF;
} else {
s[0] = (val >> 24) & 0xFF;
s[1] = (val >> 16) & 0xFF;
s[2] = (val >> 8) & 0xFF;
s[3] = (val >> 0) & 0xFF;
}
return s;
}
​
int main() {
std::cout << "[*] Initializing tables..." << std::endl;
precompute_acc();
​
// 1. 快速验证：检查 "flag" 是否匹配第一个块
// "flag" -> 0x67616C66 (Little Endian) 或 0x666C6167 (Big Endian)
uint32_t test_le = 0x67616C66; 
uint32_t test_be = 0x666C6167;
std::cout << "[?] Check logic: 'flag' encrypts to:" << std::endl;
std::cout << "    LE input -> " << std::hex << encrypt_core(test_le) << std::endl;
std::cout << "    BE input -> " << std::hex << encrypt_core(test_be) << std::endl;
std::cout << "    Target 0 -> " << std::hex << TARGETS[0] << std::endl;
std::cout << "------------------------------------------------" << std::endl;
​
std::cout << "[*] Starting brute force (Space: ~81M)..." << std::endl;
// 存储结果：key 是 target 索引, value 是解出的字符串
std::string results[6];
int found_count = 0;
​
// 4层循环穷举 (c0 c1 c2 c3)
// 假设输入是 "ABCD"，我们构建两个整数：
// LE_VAL = 0x44434241 (x86常用)
// BE_VAL = 0x41424344 (网络序/Z3脚本常用)
// 优化：并行计算 (如果编译器支持 OpenMP)
#pragma omp parallel for collapse(2)
for (int c0 = 32; c0 <= 126; c0++) {
for (int c1 = 32; c1 <= 126; c1++) {
for (int c2 = 32; c2 <= 126; c2++) {
for (int c3 = 32; c3 <= 126; c3++) {
// 构建两种字节序的整数
uint32_t val_be = (c0 << 24) | (c1 << 16) | (c2 << 8) | c3;
uint32_t val_le = (c3 << 24) | (c2 << 16) | (c1 << 8) | c0;
​
// 计算加密
uint32_t enc_be = encrypt_core(val_be);
uint32_t enc_le = encrypt_core(val_le);
​
// 检查是否命中目标
for (int i = 0; i < 6; i++) {
if (enc_le == TARGETS[i]) {
// 命中 LE 模式
char buf[5] = {(char)c0, (char)c1, (char)c2, (char)c3, 0};
#pragma omp critical
{
std::cout << "[+] Found Chunk [" << i << "] (LE Mode): " << buf << std::endl;
results[i] = buf;
found_count++;
}
}
else if (enc_be == TARGETS[i]) {
// 命中 BE 模式
char buf[5] = {(char)c0, (char)c1, (char)c2, (char)c3, 0};
#pragma omp critical
{
std::cout << "[+] Found Chunk [" << i << "] (BE Mode): " << buf << std::endl;
results[i] = buf;
found_count++;
}
}
}
}
}
}
}
​
std::cout << "[*] Done." << std::endl;
std::cout << "Final Flag: ";
for(int i=0; i<6; i++) std::cout << (results[i].empty() ? "????" : results[i]);
std::cout << std::endl;
​
return 0;
}

运行完就是flag{Fl0weRTeAVM15E3}