
文章描述了多个网络安全与数据处理挑战:分析网恋聊天记录提取隐藏信息、恢复勒索病毒数据、分解私钥恢复种子、解决矩阵与线性方程组问题及提取数字水印定位资产。 2025-9-13 15:13:0 Author: www.cnblogs.com(查看原文) 阅读量:17 收藏
数据传输-网恋需谨慎:
你是一个管理员,在一个名为orwell.freenode.net的服务器上结识了用户RiotCard85,RiotCard85主动联系了你,询问近况并提到他最近在做一个项目想让你看看。项目中隐藏了一些有趣的信息和内容,不幸的是黑客截获了你们的的网恋聊天记录,请分析找出RiotCard85留下的有趣的信息,帮助他尽快消除这些隐私泄露,SSH账号密码为ctf/123456,flag为flag{md5(题目中获取的有效flag信息)},md5默认为32位小写。


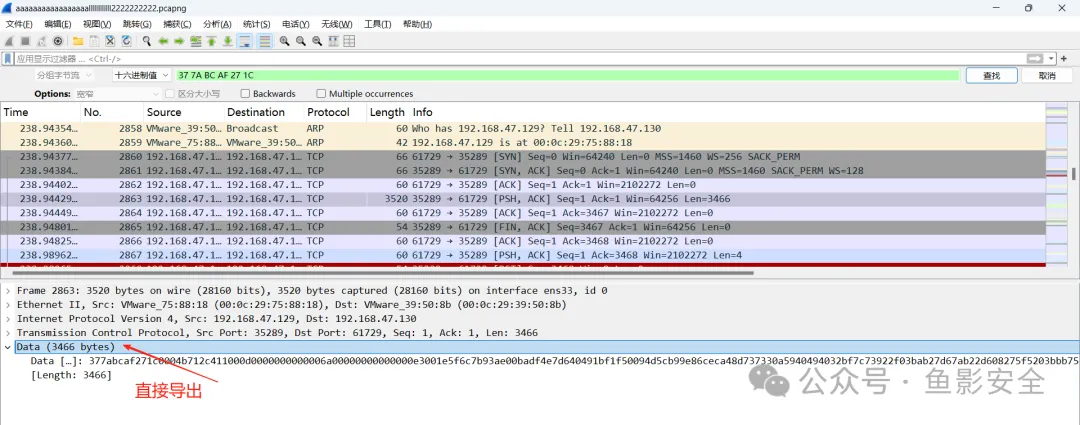

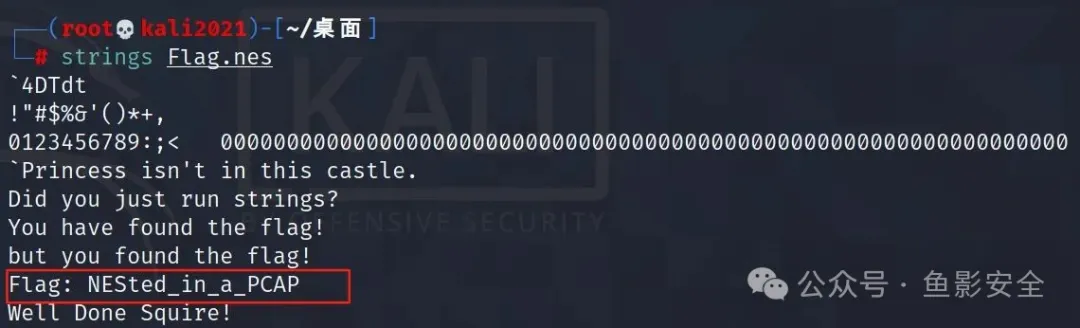

拖到nes模拟器,得到flag
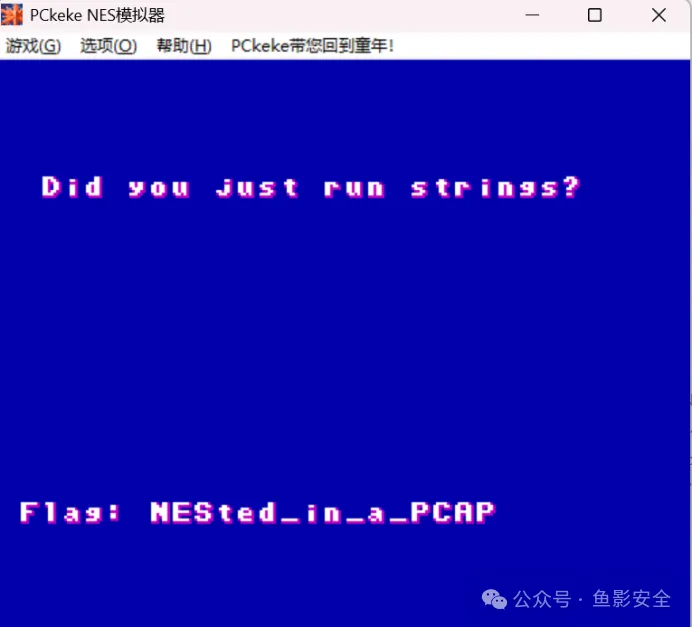
Flag:NESted_in_a_PCAP
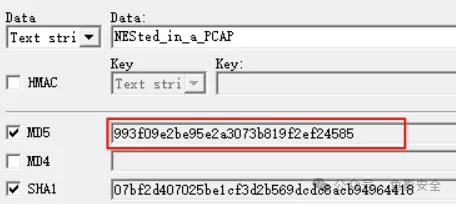
flag{993f09e2be95e2a3073b819f2ef24585}勒索病毒数据恢复场景:
通过初步排查,发现存在大量SSH登录日志,请筛查SSH日志,找出境外攻击者的IP。SSH登录信息:ctf/123456 提交格式为flag{md5(ip)}


flag{17be68c6011ca57cbe87b3256e65702f}数据加密解密-损坏的签名也不能泄露:
题目描述:在计算机飞速发展的情况下,数据安全变得尤为重要,我们采用更为安全的非对称加密对数据进行处理,这使得对于私钥的管理变得更为严格,意外泄露私钥签名,会带来巨大的数据安全隐患。
first blood
n,e,d。然后找一个网上已知n,e,d分解n的模板进行分解即可得到:p = 101847683421654680716375842695034943233474607295920357073189009241656737716914371690243711460398867127651266347312129924919977661218999208063330343536013922323662312399299474655370999029196885945932836549374793299266781427165928628878598475537865329482879199651690967937724199458455481792004282475605823232563q = 163210729062940435641851566626943305331251877830909198443806240864198682758985962110875675836580622882438335913592229471847355588617787116228491327914590616301603257385538591488022620864955374260532671790453204386239739135973102414175524438716221979798897211790763739046103381955260186638088754228604073920479
from hashlib import md5
import json
import gmpy2
def obscure_calculation(p, enc, x, y, z):
# Initialize structures with meaningless names
Omega = [[0]*100 for _ in range(100)]
Theta = [0]*100
for j_prime in range(100):
# ---- Phase 1: Obfuscated Sj calculation ----
temp_list = [gmpy2.mpz(v) for v in x[j_prime]]
sigma = sum(temp_list)
delta = gmpy2.mpz(enc[j_prime]) - sigma
Theta[j_prime] = int(delta % p) if p else 0
# ---- Phase 2: Confusing counting ----
occurrence_matrix = [[0]*10 for _ in ' '*10]
for pair in zip(y[j_prime], z[j_prime]):
occurrence_matrix[pair[0]][pair[1]] += 1
# ---- Phase 3: Nonlinear column filling ----
position_counter = 0
for first_dim in range(10):
for second_dim in range(10):
Omega[j_prime][position_counter] = int(
occurrence_matrix[first_dim][second_dim]
)
position_counter += 1
if position_counter >= 100:
break
if position_counter >= 100:
break
return Omega, Theta
p = 101847683421654680716375842695034943233474607295920357073189009241656737716914371690243711460398867127651266347312129924919977661218999208063330343536013922323662312399299474655370999029196885945932836549374793299266781427165928628878598475537865329482879199651690967937724199458455481792004282475605823232563
q = 163210729062940435641851566626943305331251877830909198443806240864198682758985962110875675836580622882438335913592229471847355588617787116228491327914590616301603257385538591488022620864955374260532671790453204386239739135973102414175524438716221979798897211790763739046103381955260186638088754228604073920479
f = open('out.json','rb').read()data = json.loads(f)
x = data['x']
y = data['y']
z = data['z']
enc = data['enc']
A_matrix = matrix(Zmod(p),A)
S_vector = vector(Zmod(p),S)
W = A_matrix.solve_right(S_vector)
seeds = []
for i in range(10):
R.<x> = PolynomialRing(Zmod(p))
f = x^5 - W[10*i + i]
seeds.append(int(f.roots()[0][0]))
recover_seed = []
hex_table = b"0123456789abfedf"
low_table = [i for i in range(1000)]
def get_seed(c):
for low in low_table:
for f in hex_table:
i = c - f + low
if (i % 1000) == low:
recover_seed.append(chr(f))
return
for i in range(10):
get_seed(seeds[i])
seed = ''.join(recover_seed)
flag = f"flag{{{md5(str(seed).encode()).hexdigest()}}}"print(flag)
@font-face{font-family:"Times New Roman";
}
@font-face{font-family:"宋体";
}
@font-face{font-family:"Calibri";
}
p.MsoNormal{mso-style-name:正文;
mso-style-parent:"";
margin:0pt;
margin-bottom:.0001pt;
mso-pagination:none;
text-align:justify;
text-justify:inter-ideograph;
font-family:Calibri;
mso-fareast-font-family:宋体;
mso-bidi-font-family:'Times New Roman';
font-size:10.5000pt;
mso-font-kerning:1.0000pt;
}
p.15{mso-style-name:内容块-16-a;
mso-style-next:正文;
margin-right:17.8500pt;
margin-left:17.8500pt;
border-top:1.0000pt solid rgb(245,247,252);
mso-border-top-alt:0.5000pt solid rgb(245,247,252);
border-right:1.0000pt solid rgb(245,247,252);
mso-border-right-alt:0.5000pt solid rgb(245,247,252);
border-bottom:1.0000pt solid rgb(245,247,252);
mso-border-bottom-alt:0.5000pt solid rgb(245,247,252);
border-left:1.0000pt solid rgb(245,247,252);
mso-border-left-alt:0.5000pt solid rgb(245,247,252);
padding:10pt 17pt 10pt 17pt ;
mso-pagination:none;
text-align:justify;
text-justify:inter-ideograph;
vertical-align:middle;
background:rgb(245,247,252);
font-family:Calibri;
mso-fareast-font-family:宋体;
mso-bidi-font-family:'Times New Roman';
font-size:10.5000pt;
mso-font-kerning:1.0000pt;
}
span.msoIns{mso-style-type:export-only;
mso-style-name:"";
text-decoration:underline;
text-underline:single;
color:blue;
}
span.msoDel{mso-style-type:export-only;
mso-style-name:"";
text-decoration:line-through;
color:red;
}
@page{mso-page-border-surround-header:no; mso-page-border-surround-footer:no;}@page Section0{margin-top:72.0000pt;
margin-bottom:72.0000pt;
margin-left:90.0000pt;
margin-right:90.0000pt;
size:595.3000pt 841.9000pt;
layout-grid:15.6000pt;
mso-header-margin:42.5500pt;
mso-footer-margin:49.6000pt;
}
div.Section0{page:Section0;}flag{a2517703dcc32c46b263e13d9753d2eb}Crypto-还会在见面吗?:
题目描述:海很小,小到可以从巨人的眼里流出。曾经和过往变得很矮,矮到我跪下,头磕在地上也比我矮。我们发现了一种矩阵与线性方程组,所以逆转时间的公式是什么,我想你会找到她
1.自定义代数环元素 T(a1,a2) ,加法取元素最大值,乘法采用最大和组合。
2.通过爆破 k,l,r,sk,l,r,sk,l,r,s 指数和偏移 p,qp,qp,q,
使得矩阵关系 KA=KBK_A = K_BKA=KB 成立。
3.用满足关系的矩阵 KAK_AKA 的字符串MD5作为AES-128密钥。
4.AES-ECB模式解密密文得到flag
参考https://eprint.iacr.org/2024/010.pdf 来攻击即可
手动处理一下数据类型,enc删一下转义字符
数据水印-这么美这么近周末玩水印:
数字资产是新时代计算机飞速发展过程中的产生的无形资产,应进行妥善保管,为防止他人盗取,篡改视频和图片,我们引进水印技术来保障资产的不可否认性。小宁未妥善保管个人数字资产,将自己的位置信息泄露出来,你能通过逐步分析找到他吗?作为奖励,flag为flag{md5(所在位置)}。md5默认为32位小写,温馨提示:位置要精确到门牌号哦!!!
给了一张图片和加密的压缩包
foremost 分离得到9张图 聪明的小伙伴看到9直接可以想到二维码
直接工具一把梭 得到8张二维码,
然后ps拼接一下 像素块需要写脚本

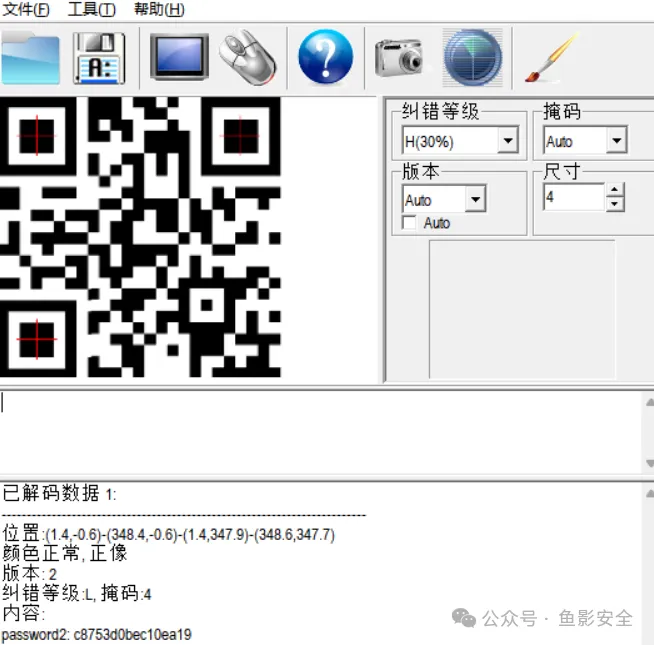
最后拼接得到二维码QR扫码
得到password2: c8753d0bec10ea19
但是这个是pss2需要找1 ,使用水印提取 得到pss1
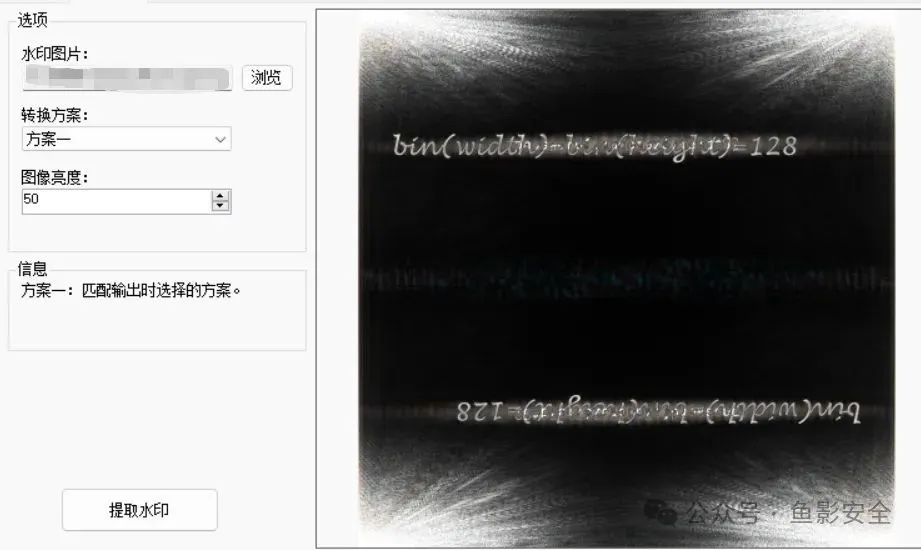
最终提取出password1: 7ddcf32671e7d45



flag{a846c0e291527639baa3f78a1d231db6}
如有侵权请联系:admin#unsafe.sh