SECCON Beginners CTF 2025 writeup

SECCON Beginners CTF 2025のCrypto問題のwriteupです。

seesaw
01-Translator
elliptic4b
Golden Ticket
mathmyth

seesaw

import os
from Crypto.Util.number import getPrime

FLAG = os.getenv("FLAG", "ctf4b{dummy_flag}").encode()
m = int.from_bytes(FLAG, 'big')

p = getPrime(512)   
q = getPrime(16)
n = p * q
e = 65537
c = pow(m, e, n)

print(f"{n = }")
print(f"{c = }")

qが16bit程度しかないので素因数分解できます。↓のscriptではlimit書いてるけどいらないと思う

f = open("output.txt")

n = int(f.readline().strip().split(" = ")[1])
c = int(f.readline().strip().split(" = ")[1])

((p, _), (q, _)) = factor(n, limit=2**17)
d = pow(65537, -1, (p-1)*(q-1))
m = pow(c, d, n)

print(bytes.fromhex(hex(m)[2:]))

01-Translator

import os
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad
from Crypto.Util.number import bytes_to_long


def encrypt(plaintext, key):
    cipher = AES.new(key, AES.MODE_ECB)
    return cipher.encrypt(pad(plaintext.encode(), 16))

flag = os.environ.get("FLAG", "CTF{dummy_flag}")
flag_bin = f"{bytes_to_long(flag.encode()):b}"
trans_0 = input("translations for 0> ")
trans_1 = input("translations for 1> ")
flag_translated = flag_bin.translate(str.maketrans({"0": trans_0, "1": trans_1}))
key = os.urandom(16)
print("ct:", encrypt(flag_translated, key).hex())

フラグがサーバ側でバイナリ文字列に変換されたあと、更にユーザの入力に応じて0 1 をそれぞれ好きな文字列に置換できます。その後置換後の文字列をAESのECBモードで暗号化されたものが渡されます。

ECBモードをみると、同じ平文ブロックを暗号化すると同じ暗号文になるという性質を思い出すので、これを利用したくなります。具体的には0, 1 をそれぞれ適当な1ブロックに置換すると、暗号文全体は0 を暗号化したブロックと1を暗号化したブロックからなり、その2種類だけ*1となるので平文を復元できます。

from ptrlib import Socket, chunks



sock = Socket("nc 01-translator.challenges.beginners.seccon.jp 9999")

sock.sendlineafter("0> ", "0" * 16)
sock.sendlineafter("1> ", "1" * 16)

ct = sock.recvlineafter("ct:").decode().strip()
cs = chunks(ct, 32)

flag = 0
for c in cs[:-1]:  
    if c == cs[0]:
        flag = flag*2 + 1
    else:
        flag = flag*2
print(bin(flag))
print(bytes.fromhex(hex(flag)[2:]))

elliptic4b

import os
import secrets
from fastecdsa.curve import secp256k1
from fastecdsa.point import Point

flag = os.environ.get("FLAG", "CTF{dummy_flag}")
y = secrets.randbelow(secp256k1.p)
print(f"{y = }")
x = int(input("x = "))
if not secp256k1.is_point_on_curve((x, y)):
    print("// Not on curve!")
    exit(1)
a = int(input("a = "))
P = Point(x, y, secp256k1)
Q = a * P
if a < 0:
    print("// a must be non-negative!")
    exit(1)
if P.x != Q.x:
    print("// x-coordinates do not match!")
    exit(1)
if P.y == Q.y:
    print("// P and Q are the same point!")
    exit(1)
print("flag =", flag)

ランダムな $y$ が渡されて、 $P = (x, y)$ がsecp256k1 上の点になるように $x$ を渡した後、 $Q = aP$ が $P$ と異なる $x$ 座標を持ち、 $P$ と同じ $y$ 座標をもつように $a$ をうまく選べれば勝ち、となります。

まず $y$ 座標から $x$ 座標を求める必要がありますが、これは楕円曲線の式 $y^2 \equiv x^3 + ax + b \mod p$ を満たすように式に $a, b, y$ を代入して $x$ を求めればよいです。

続いていい $a$ を求めます。まずそもそも同一の楕円曲線上にy座標が同じでx座標が異なる2つの点が存在するのか、という話ですが、存在します。平面座標上での楕円曲線の形を思い出すと $P$ と $-P$ がまさにそういう点ですね。もはや常識。

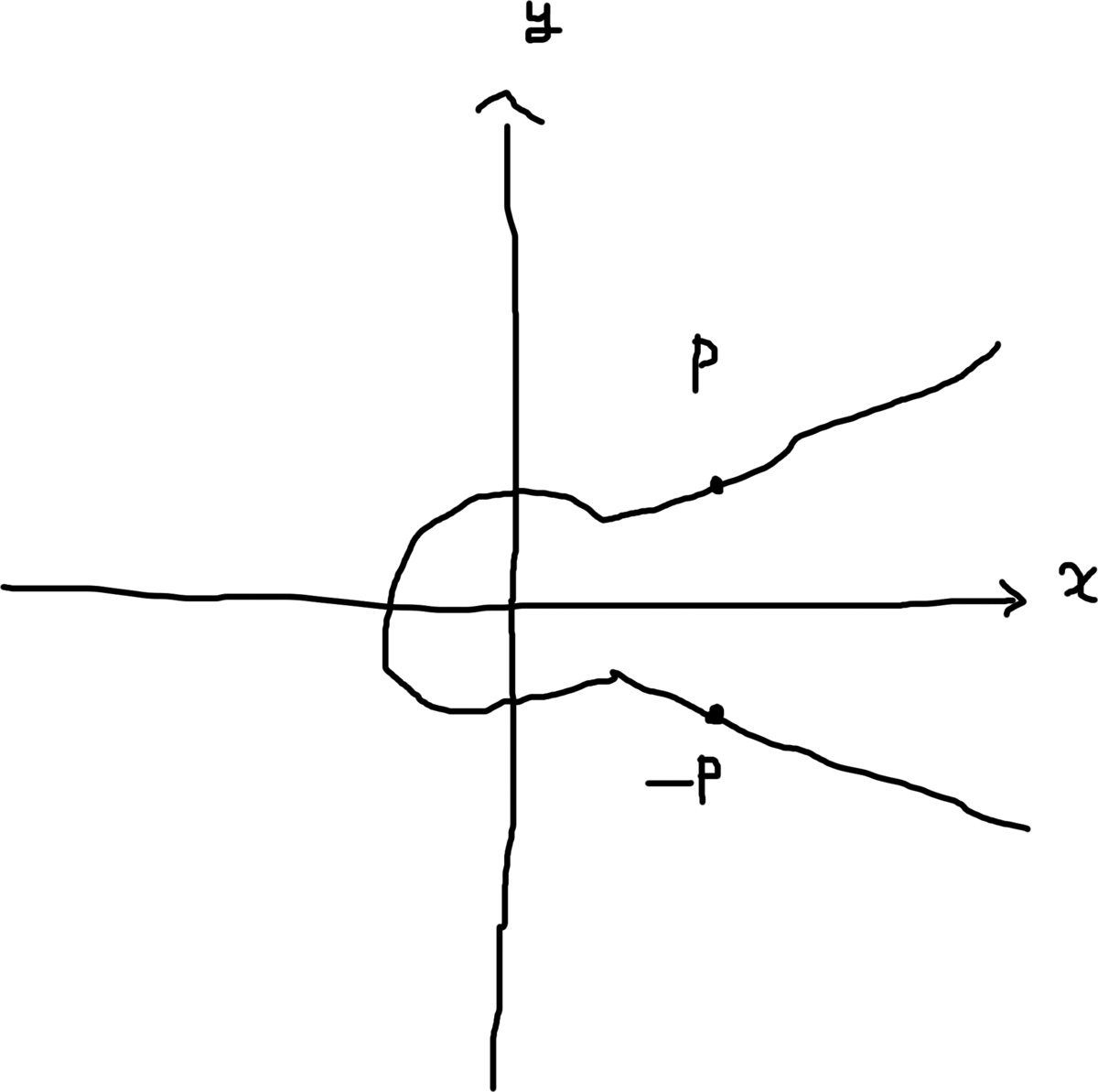
ということは $a = -1$ とすれば良さそうですが、入力の制約により $a$ はnon negativeな値である必要があるのでかわりに $-1 \pmod{\#E}$ を利用します（ $\#E$ は楕円曲線 $E$ の位数）

from ptrlib import Socket

p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
K = GF(p)
a = K(0x0000000000000000000000000000000000000000000000000000000000000000)
b = K(0x0000000000000000000000000000000000000000000000000000000000000007)
E = EllipticCurve(K, (a, b))
G = E(0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798, 0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)
E.set_order(0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141 * 0x1)

PR.<x> = PolynomialRing(K)

while True:
    
    sock = Socket("nc elliptic4b.challenges.beginners.seccon.jp 9999")
    y = int(sock.recvlineafter("y = "))
    f = y**2 - (x**3 + a*x + b)
    roots = f.roots() 
    if len(roots) != 0:
        break

x = roots[0][0]
G1 = E((x, y))

inv = Zmod(E.order())(-1)
G2 = inv *G1
assert G1[0] == G2[0]

sock.sendlineafter("x = ", str(x))
sock.sendlineafter("a = ", str(inv))
sock.interactive()

Golden Ticket

問題のスクリプトはやや長いので省略。encryption ticketを利用するとEnc(key, iv, input || pad) がえられるオラクルが利用でき、decryption ticketを利用するとDec(key, iv, input || pad)が得られるオラクルが利用できます。Enc, Dec AES-CBCによる暗号化・復号で、どちらもinput は16バイト（1ブロック）までで、それぞれ3回まで利用できます。

目的は 6ブロックのランダムな文字列 challenge に対して、Dec(key, iv', payload) == challenge となるような iv', payload を求めることです。

まずはivを求めます。ここで2回オラクルを使う方法を考えていて時間を溶かしていたけど、input == padとなるようにinputを決めて（つまり input = 0x10101010...10）decryption ticketを利用すると、1ブロック目は 0x1010...10 をAESで復号したものにIVをXORした値、2ブロック目は 0x1010...10 をAESで復号したものに1ブロック目の平文、0x1010...10 をXORした値、となります。

ここからは $Enc, Dec$ はAESによる1ブロックのみの暗号化を表すことにすると、1ブロック目は $Dec(0x1010...10) \oplus IV$ 、2ブロック目は $Dec(0x1010...10) \oplus 0x1010...10$ となります。2ブロック目の結果から $Dec(0x1010...10)$ がわかるので、1ブロック目の結果にXORすると $IV$ が手に入ります。

$IV$ がわかったので、これを利用してencryption ticketやdecryption ticketを利用すると何ができるかを考えます。encryption ticketを利用するとCBCモードの復号における前ブロックの暗号文 $c_{i - 1}$ が決まっているとき、そのブロックの復号結果を望む値 $t_{i}$ にするような暗号文のブロック $c_{i}$ を求めることができます。

また、decryption ticketを利用すると、CBCモードのそのブロックの暗号文 $c_{i}$ が決まっているとき、そのブロックの復号結果を望む値 $t_{i}$ にするような前の暗号文のブロック $c_{i}$ を求めることができます。

あとはこのパーツを組み合わせて6ブロックを作ればよいです。ここはencryptioin oracleとdecryption oracleの並べ方……みたいな話題はあるのですが、考えるときは↓みたいな図を書いてDec→DecとかEnc→Encという並べ方が良さそう、みたいなことを考えるものの、説明のときはスクリプトを見るのが早そうなのでそれを貼るだけにします

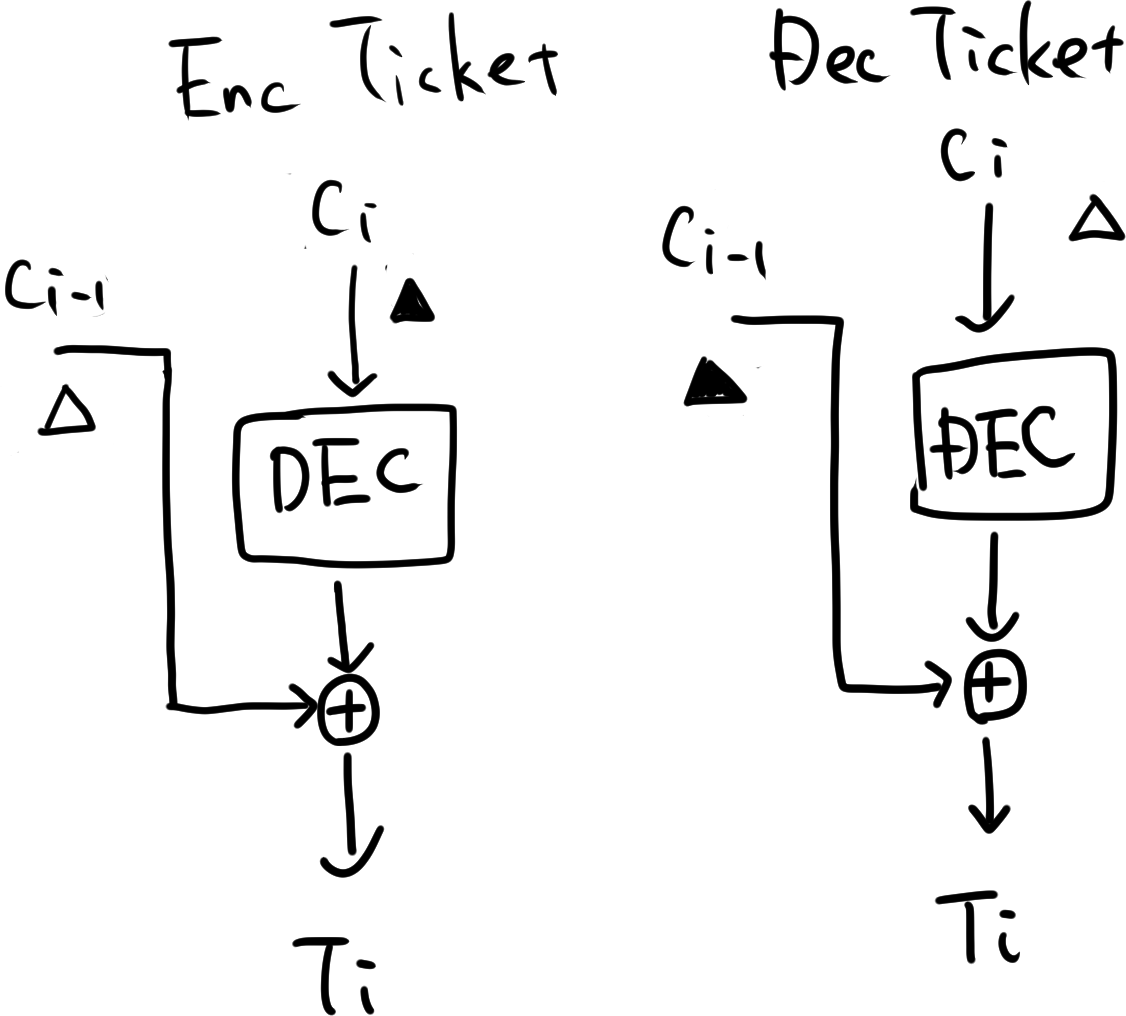
△を決めると▲が求められるという順番なので、▲が重複してはいけない……のように考えていた図

from ptrlib import Socket, chunks, xor


sock = Socket("nc golden-ticket.challenges.beginners.seccon.jp 9999")

def get_challenge():
    sock.sendlineafter("> ", "3")
    chal = bytes.fromhex(sock.recvlineafter("challenge:").decode().strip())
    sock.sendlineafter("answer> ", "00")
    return chunks(chal, 16)

def enc_oracle(payload: bytes):
    sock.sendlineafter("> ", "1")
    sock.sendlineafter("pt> ", payload.hex())
    pt = bytes.fromhex(sock.recvlineafter("ct: ").decode().strip())
    return chunks(pt, 16)


def dec_oracle(payload: bytes):
    sock.sendlineafter("> ", "2")
    sock.sendlineafter("ct> ", payload.hex())
    pt = bytes.fromhex(sock.recvlineafter("pt: ").decode().strip())
    return chunks(pt, 16)



dec16_iv, dec16_16 = dec_oracle(bytes([16] * 16))
dec16 = xor(dec16_16, bytes([16] * 16))
iv = xor(dec16_iv, dec16)
print(f"iv={iv.hex()}")


def find_c_from_prev_c(prev_c: bytes, t: bytes):
    """
    find c_{i} from c_{i-1} and t_{i}
    which satisfies Dec(c_{i}) ^ c_{i-1} = t_{i}
    use 1 encryption ticket
    """
    x, _ = enc_oracle(xor(xor(prev_c, t), iv))
    return x

def find_prev_c_from_c(c: bytes, t: bytes):
    """
    find c_{i-1} from c_{i} and t_{i}
    which satisfies Dec(c_{i}) ^ c_{i-1} = t_{i}
    using 1 decryption ticket
    """
    x, _ = dec_oracle(c)
    return xor(xor(x, iv), t)




T_1, T_2, T_3, T_4, T_5, T_6 = get_challenge()


C_3 = bytes([16] * 16)
C_2 = xor(dec16, T_3)
C_1 = find_prev_c_from_c(C_2, T_2)
IV_ = find_prev_c_from_c(C_1, T_1)

C_4 = find_c_from_prev_c(C_3, T_4)
C_5 = find_c_from_prev_c(C_4, T_5)
C_6 = find_c_from_prev_c(C_5, T_6)


payload = IV_ + C_1 + C_2 + C_3 + C_4 + C_5 + C_6
sock.sendlineafter("> ", "3")
sock.sendlineafter("answer> ", payload.hex())
print(sock.recvline().decode().strip())  


sock.sendlineafter("> ", "4")
sock.interactive()

ticketの数がぎりぎりに調整されていて、よくできた問題だと思います。今回のセットで一番面白い問題でした。

mathmyth

RSAで280bitの $q$ に対して、 $p$ は224bitの素数 $r$ , $r_2 = r + \alpha$ , 512bitの乱数 $s$ を用いて $p = q^2r_2 + rs$ と表される素数で、 $n = pq, e, c, r$ が与えられる、という問題です。

$n$ を展開すると $q^3r_2 + qrs$ となって $q^3$ の影響が大きそうです。 $r \simeq r_2$ なので $r$ で割っておいて $q' = \left(\frac{n}{r}\right)^{1/3}$ とすると $q \approx q'$ が成り立ちます。

どのくらい近いのか手元で適当な値を生成して実験すると $d = q' - q$ は大体240bit程度ということがわかります*2。この値は $r$ と割と大きさが近いので $d_r = d \mod r$ を考えると、 $d = d_r + rk$ を満たすような $k$ はせいぜい10bitかそこらです。つまり、 $d \mod r$ を求められたら $d$ を探索し、そこから $q = q' - d$ と計算できそうです。

では $d \mod r$ を計算できるのかというと、 $q'$ は知っているので $q \mod r$ がわかればよいです。これは $n \mod r$ を考えると $n \equiv q^3\alpha \mod r$ 、更に $\alpha$ は求められるので $\alpha^{-1}$ をかけてこれの影響も消して $q^3 \mod r$ 、 $r$ は素因数が小さくて素因数分解できるので三乗根が計算できて $q \mod r$ ……と求められます。

f = open("output.txt")

n = int(f.readline().strip().split(" = ")[1])
e = int(f.readline().strip().split(" = ")[1])
c = int(f.readline().strip().split(" = ")[1])
r = int(f.readline().strip().split(" = ")[1])

r2 = next_prime(r)
a = r2 - r


q3r = n % r * Zmod(r)(a).inverse()  

ns = ecm.factor(r)
all_roots = []
for p in ns:
    roots = GF(p)(q3r).nth_root(3, all=True)
    all_roots.append([int(root) for root in roots])

import itertools
root_combinations = list(itertools.product(*all_roots))
q_r_list = [crt(list(c), ns) for c in root_combinations]




q_max = floor((Integer(n) / r)**(1/3))

for q_r in q_r_list:
    q_delta_r = (q_max - q_r) % r
    print(q_max)
    print(q_delta_r)

    
    for k in range(2048):
        q = q_max - (int(q_delta_r) + k*r)
        if n % q == 0:
            print(f"[+] {q=}")
            break
    else:
        continue

    p = n // q
    d = pow(e, -1, (p-1)*(q-1))
    m = pow(c, d, n)

    print(bytes.fromhex(hex(m)[2:]))

これもなかなかおもしろかったのですが、フラグでAIに解かれた、と書いてあってそれに対してどのように考えているのか、なぜわざわざそのような文言のフラグにしたのか、この問題のdifficultyがhardであることとなにか関係があるのかが気になりました。Beginnersくらいの問題はAIが全部解けちゃうよね、ということでしょうか*3