Table of Links

Abstract and 1. Introduction

1.1 A Polyethylene-based metamaterial for acoustic control

2 Relaxed micromorphic modelling of finite-size metamaterials

2.1 Tetragonal Symmetry / Shape of elastic tensors (in Voigt notation)

3 Dispersion curves

4 New considerations on the relaxed micromorphic parameters

4.1 Consistency of the relaxed micromorphic model with respect to a change in the unit cell’s bulk material properties

4.2 Consistency of the relaxed micromorphic model with respect to a change in the unit cell’s size

4.3 Relaxed micromorphic cut-offs

5 Fitting of the relaxed micromorphic parameters: the particular case of vanishing curvature (without Curl P and Curl P˙)

5.1 Asymptotes

5.2 Fitting

5.3 Discussion

6 Fitting of the relaxed micromorphic parameters with curvature (with Curl P)

6.1 Asymptotes and 6.2 Fitting

6.3 Discussion

7 Fitting of the relaxed micromorphic parameters with enhanced kinetic energy (with Curl P˙) and 7.1 Asymptotes

7.2 Fitting

7.3 Discussion

8 Summary of the obtained results

9 Conclusion and perspectives, Acknowledgements, and References

A Most general 4th order tensor belonging to the tetragonal symmetry class

B Coefficients for the dispersion curves without Curl P

C Coefficients for the dispersion curves with P

D Coefficients for the dispersion curves with P

6 Fitting of the relaxed micromorphic parameters with curvature (with Curl P)

6.1 Asymptotes

Because the cut-offs are independent of the coefficients with higher order of k, they do not change with the addition of Curl P. Instead, the expressions of the asymptotes hugely differ compared to the expression without Curl P discussed before. We only include the terms with the highest order of k available and compute

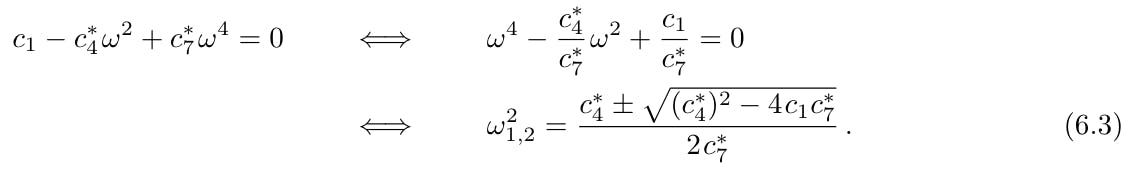
Surprisingly, the asymptotes with Curl P are significantly simpler because we must only solve a second-order polynomial instead of a third-order polynomial needed for the cut-offs and the asymptotes without Curl P. We now only have four distinct horizontal asymptotes (two shear and two pressure) in contrast to six before, which means that we must allow that the two curves (one shear and one pressure) will tend to infinity for high values of k, and our choice falls on the two highest optic curves. The same reasoning about the use of the asymptote in Section 5.1 is applied here besides for the two highest optic curves that do not have a horizontal asymptote.

6.2 Fitting

Although the expressions of the asymptotes are different from the ones without the Curl P, we still have the same split between the parameters, resulting in 4 independent parameters for every group of asymptotes, cf. Table 7.

We list the numerical values of all parameters used for the fitting of the micromorphic model in Table 8.

6.3 Discussion

Most other values remain at the same magnitude but are slightly higher, cf, Table 9. In future works, we will consider an enhanced relaxed micromorphic model to better describe these effects.