Table of Links

Abstract and 1 Introduction

2 Background

2.1 Data Augmentation

2.2 Anchor Regression

3 Anchor Data Augmentation

3.1 Comparison to C-Mixup and 3.2 Preserving nonlinear data structure

3.3 Algorithm

4 Experiments and 4.1 Linear synthetic data

4.2 Housing nonlinear regression

4.3 In-distribution Generalization

4.4 Out-of-distribution Robustness

5 Conclusion, Broader Impact, and References

A Additional information for Anchor Data Augmentation

B Experiments

4.2 Housing nonlinear regression

We extend the results from the previous section to the California and Boston housing data and compare ADA to C-Mixup [49]. We repeat the same experiments on three different regression datasets. Results are provided in Appendix B.2 and also show the superiority of ADA over C-Mixup for data augmentation in the implemented experimental setup.

Data: We use the California housing dataset [19] and the Boston housing dataset [14]. The training dataset contains up to n = 406 samples, and the remaining samples are for validation. We report the results as a function of the number of training points.

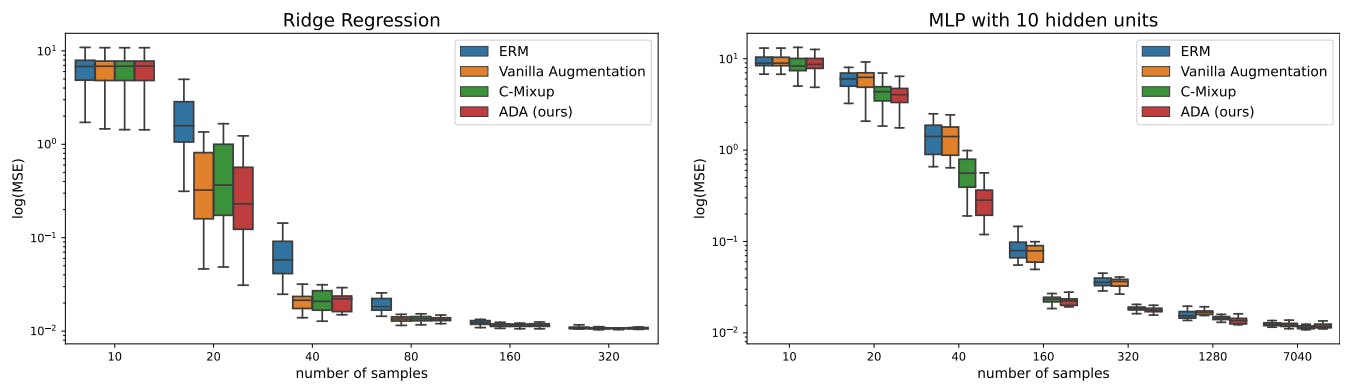
Models and comparisons: We fit a ridge regression model (baseline) and train a MLP with one hidden layer with a varying number of hidden units with sigmoid activation. The baseline models only use only the original data. We train the same models using C-Mixup with a Gaussian kernel and bandwidth of 1.75. We compare the previous approaches to models fitted on ADA augmented data. We generate 20 different augmentations per original observation using different values for γ controlled via α = 4 similar to what was described in Section 4.1. The Anchor matrix is constructed using k-means clustering with q = 10.

Results: We report the results in Figure 3. First, we observe that the MLPs outperform Ridge regression suggesting a nonlinear data structure. Second, when the number of training samples is low, applying ADA improves the performance of all models compared to C-Mixup and the baseline. The performance gap decreases as the number of samples increases. When comparing C-Mixup and ADA, we see that using sufficiently many samples both methods achieve similar performance. While on the Boston data, the performance gap between the baseline and ADA persists, on California housing, the non-augmented model fit performs better than the augmented one when data availability increases. This suggests that there is a sweet spot where the addition of original data samples is required for better generalization, and augmented samples cannot contribute any further.