Google Capture The Flag 2024 IDEA writeup

今年のGoogle Capture The Flagにはkijitora というチームで出ました。2022年のGoogle CTFに合わせて結成された連合チームで、このときはまだ私もCTFやっているという感じだったので末席に名を連ねていました。このときにdiscordサーバにjoinしていたことで今年もしれっと参加が許されて、今年は真面目にやったのでDESFUNCTIONALという問題とIDEAという問題を協力しながら解きました。IDEAは結局4チームしか解けてない難しい問題だけど粘った結果解けたので、writeupです。

TL; DR
問題概要
- IDEA について
KとK⊕2103の関連鍵攻撃 (k_18, k_20の導出)
KとK⊕2127の関連鍵攻撃 (k_19, k_21の導出)
- 誕生日攻撃によるgood pairの収集
- 中間一致攻撃によるk_19, k_21 の特定
32bit全探索によるk_16, k_17の特定
32bit全探索による暗号鍵の復元
コードすべて
感想

TL; DR

スーパーヒューリスティックで粘って鍵をちょっとずつ求めて、残り32bitになったら全探索

問題概要

IDEAというブロック暗号が実装されている。通常は8.5ラウンドのところ、3.5ラウンドのみの実装になっている
サーバに接続すると次のことができる。コストが2024を超えるか、サーバに接続後512秒が経過したら挑戦失敗で、暗号化に使われている128ビットの鍵を当てることができればフラグがもらえる
- 暗号化 : コスト1
- ビット反転：コスト=反転するbit数*100
  - 鍵の好きなbitを反転できる。以後の暗号化では反転操作を行った鍵が使われる

IDEA について

wikipediaに載っているのでこれを参照されたい。以下ではこのwriteupで使う話だけを説明する。

ja.wikipedia.org

鍵が128ビット、1ブロックが64ビットのブロック暗号。暗号化処理中は平文、鍵を16ビット単位の4つ組（鍵は6つ組）として扱い、KAという操作とMAという操作からなるラウンド操作を繰り返し行うことで暗号化する。 $k$ ラウンド目の入力を $(X^{(k)}_{1}, X^{(k)}_{2}, X^{(k)}_{3}, X^{(k)}_{4})$ と表すことにし、 $k$ ラウンド目で利用されるラウンド鍵を $(Z^{(k)}_{1}, Z^{(k)}_{2}, Z^{(k)}_{3}, Z^{(k)}_{4}, Z^{(k)}_{5}, Z^{(k)}_{6})$ と表すことにする*1。ラウンド鍵の導出についてはあとで説明する。

KAは次のような操作である（出力を $Y^{(k)}_{1}, Y^{(k)}_{2}, Y^{(k)}_{3}, Y^{(k)}_{4})$ とする）

$\require{color}$

MAは次のような操作である（出力は、次のKAの入力となるので $(X^{(k+1)}_{1}, X^{(k+1)}_{2}, X^{(k+1)}_{3}, X^{(k+1)}_{4})$ と書いた）

ただし $p^{(k)} = Y^{(k)}_{1} \oplus Y^{(k)}_{3}, q^{(k)} = Y^{(k)}_{2} \oplus Y^{(k)}_{4}$ として、

である。

ここで、 $\boxplus$ は $\mod 2^{16}$ 上での加算、 $\odot$ は $\mod 2^{16} + 1$ 上での乗算*2、 $\oplus$ はビットごとの排他的論理和である。

また、暗号化の最後にはハーフラウンドがある。これはKAと酷似したKA'という処理によって行われる*3。

KA':

ラウンド鍵はマスター鍵の適当なビットスライスである。説明が面倒なので論文*4から表を引っ張ってくるとこういう感じ。非常にシンプルで、ラウンド鍵がわかればマスター鍵もすぐ求まる。

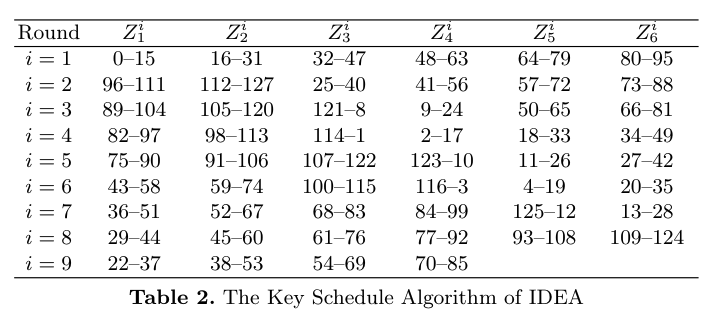
また、ラウンド鍵については0-indexedな通し番号 $k_{i}$ とも表すことにする。つまり $k_{0} = Z^{(1)}_{1}, k_{18} = Z^{(4)}_{1}$ という具合である。

KとK⊕2¹⁰³の関連鍵攻撃 (k_18, k_20の導出)

鍵の差分を打ち消すような差分を持つ平文を渡す

ビット反転という鍵の好きなビットを反転させる操作があることから、これを使うのだろうと予想して論文を探すとIDEAに対する関連鍵攻撃を説明している論文*5が見つかった。その論文によると3.5ラウンドのIDEAでは、鍵 $K$ で平文 $m$ を暗号化した結果と鍵 $K' = K\oplus 2^{103}$ で平文 $m' = m \pm 2^{39}$ を暗号化した結果の差分からいくつかのラウンド鍵を求めることができるらしい。

鍵 $K$ から導出されたラウンド鍵 $Z^{(k)}_{i}$ と鍵 $K'$ から導出されたラウンド鍵 $Z'^{(k)}_{i}$ を比較すると、鍵の値が異なるのは $(Z^{(1)}_{2}, Z'^{(1)}_{2}) (Z^{(3)}_{4}, Z'^{(3)}_{4})$ の2ペアだけで、その値もそれぞれ1bitずつしか違わない。

そして、 $Z^{(1)}_{2}, Z'^{(1)}_{2}$ が作用するのは平文の2ブロック目*6に対してであり、KAの処理をみればその作用は $\boxplus$ である。これは $\mod 2^{16}$ 上での加算にすぎないので、鍵の加算の1bit文を打ち消すような差を持つ平文を暗号化させれば1ラウンド目の暗号結果が一致する。

このような結果になる平文 $m, m'$ を鍵 $K, K'$ で暗号化すると続くラウンドでは次のようになる

k_18の導出

さて、ここで2つの暗号文について、 $k_{18}$ （すなわち $Z^{(4)}_{1}$ がわかっているという仮定をおいた状態で、1ブロック目と3ブロック目の差分（XOR）の最下位bit (LSB)を比較してみる。

まず1ブロック目について（①）。これは $Y^{(4)}_{1} = X^{(4)}_{1} \odot Z^{(4)}_{1}, Y'^{(4)}_{1} = X'^{(4)}_{1} \odot Z'^{(4)}_{1}$ だが、いま $Z^{(4)}_{1}$ （ $= Z'^{(4)}_{1}$ ）はわかっている前提なので逆数をかけて取り除いて良い。ついでに $X^{(4)}_{1}, X'^{(4)}_{1}$ は開いてしまって

$Y^{(3)}_{1} \oplus t^{(3)}, Y'^{(3)}_{1} \oplus t'^{(3)}$

がわかっている。 $Y^{(3)}_{1} = Y'^{(3)}_{1}$ なのでこれのXORをとると $t^{(3)} \oplus t'^{(3)}$ が得られる。LSBをとって①= $lsb(t^{(3)} \oplus t'^{(3)})$

続いて3ブロック目について（②）。 $Y^{(4)}_{3} = \textcolor{red}{X^{(4)}_{3}} \boxplus Z^{(4)}_{3}, Y'^{(4)}_{3} = \textcolor{red}{X'^{(4)}_{3}} \boxplus Z'^{(4)}_{3}$ だがこれも $X^{(4)}_{3}, X'^{(4)}_{3}$ を開いて $Y^{(4)}_{3} = (Y^{(3)}_{3} \oplus t^{(3)}) \boxplus Z^{(4)}_{3}, Y'^{(4)}_{3} = (Y'^{(3)}_{3} \oplus t'^{(3)}) \boxplus Z'^{(4)}_{3}$ である。

あとでLSBをとることを考えると、 $\boxplus$ と $\oplus$ は同一視できて*7 $Y^{(4)}_{3} = Y^{(3)}_{3} \oplus t^{(3)} \oplus Z^{(4)}_{3}, Y'^{(4)}_{3} = Y'^{(3)}_{3} \oplus t'^{(3)} \oplus Z'^{(4)}_{3}$ としてもよい。 $Z^{(3)}_{3} = Z'^{(3)}_{3}$ かつ $Y^{(3)}_{3} = Y'^{(3)}_{3}$ より、（LSBとって）XORを取ると②= $lsb(t^{(3)} \oplus t'^{(3)})$ 。

つまり、 $k_{18}$ がわかっているとき、①=②が成り立つ。 $k_{18}$ は16bitの値なので全探索可能だから、①=②が成り立つような値を探せばそれが $k_{18}$ である、ということになる。

当然①, ②の式の値は0か1しかないので、探索中には $k_{18}$ でない値についても①=②が成り立つことがあるが、この性質は（1ラウンド目の暗号化結果がおなじになるような）どんな $m, m'$ のペアについて成り立つので、そのような平文の組にたいする暗号文の組を複数個あつめて、すべてのケースについて成り立つ値を $k_{18}$ として採用すれば良い。

k_20の導出

$k_{18}$ がわかれば同様の議論で $k_{20}$ が導出できる。さっきはLSBを考えたが、今回はLSBを取らずに単にXORを取ることを考える。

1ブロック目については単に $\Delta t = t^{(3)} \oplus t'^{(3)}$ が得られる。3ブロック目については $k_{20}$ ( $= Z^{(4)}_{3} = Z'^{(4)}_{3}$ ) がわかっているという前提をおけば、この値を引いてXORを取れば、 $\Delta t_2 = t^{(3)} \oplus t'^{(3)}$ となるはずである。つまり、正しい $k_{20}$ について $\Delta t = \Delta t_2$ が成り立つ。これはLSBを取っているわけではないが、加算という処理が影響するビットの少なさから誤った $k_{20}$ の予想についても成り立つことがあるため、やはり複数の組すべてで成立するような値を採用すると良い。それでも2通りでてくるんですがまあ1/2であたりなので良しとする

KとK⊕2¹²⁷の関連鍵攻撃 (k_19, k_21の導出)

続いて、鍵 $K$ にたいして $K'' = K\oplus 2^{127}$ としたときの関連鍵攻撃を考える。

このとき、差分が現れるラウンド鍵は $(Z^{(1)}_{1}, Z''^{(1)}_{1}), (Z^{(3)}_{3}, Z''^{(3)}_{3}), (Z^{(4)}_{3}, Z''^{(4)}_{3})$ の3ペアである。先ほどと同様に、1ラウンド目の暗号結果が同一になるような平文のペア $(m, m'')$ を考えたいのだが、今回は1ラウンド目で差分があるラウンド鍵が乗算に使われていて、 $m$ に対して計算して $m'$ を求めることはできない。ただし、 $m'$ の2ブロック目から4ブロック目は $m$ と同じとしたうえで1ブロック目の値を $2^{16}$ 通り試せば、かならずそのような $m'$ が一つ存在する*8。今回の問題設定では $2^{16}$ 通り試すことは不可能だが、後述のように誕生日攻撃でこのような $(m, m'')$ のペア（good pairと呼ぶことにする）を得ることができる

誕生日攻撃によるgood pairの収集

ある $m$ にたいしてgood pairの片割れとなるような $m''$ が得られる確率は $1/2^{16}$ だが、いくつもの $m_1, m_2, \dots$ に対して、そのいずれかとgood pairになるような $m''$ が得られる確率はそれよりもずっと大きい*9。この性質を利用して、2, 3, 4ブロック目を固定し1ブロック目を適当に変化させた平文を鍵 $K$ のもとでいくつも暗号化しておき、 $K''$ のもとでも同様に1ブロック目だけを変化させた平文をいくつも暗号化し、あとでgood pairになっている組があるかを確かめることで、現実的な回数の暗号化オラクルの利用でgood pairとなるような組を得ることができる。

ある $(m, m'')$ がgood pairになっているかの判定は、次のようなお気持ちでやる。

これでgood pairとなるような $(m, m'')$ が求められる。

この方法でgood pairを求めると、実際にはgood pairではないがgood pairと判定されてしまうケースもそこそこある。実験した感じでは、体感50%くらいの偽陽性がある。しかしもっと良い方法は思いつかなかったのでこれで頑張った

中間一致攻撃によるk_19, k_21 の特定

さて、これでgood pairが（いくつか）求まった。ここで更に $k_{19}, k_{21}$ もわかっていると仮定する。

このとき2ブロック目について、 $Y^{(4)}_{2} = \textcolor{red}{Y^{(3)}_{2}} \oplus u^{(3)} \boxplus Z^{(4)}_{2}, Y''^{(4)}_{2} = \textcolor{red}{ Y''^{(3)}_{2}} \oplus u''^{(3) } \boxplus Z''^{(4)}_{2}$ から $k_{19} = Z^{(4)}_{2} = Z''^{(4)}_{2}$ と $Y^{(3)}_{2} = Y''^{(3)}_{2}$ をつかって $\Delta u = u^{(3)} \oplus u''^{(3)}$ が計算できる。

4ブロック目についても同様に、 $\Delta u_2 = u^{(3)} \oplus u''^{(3)}$ となるから、正しい $(k_{19}, k_{21})$ の組については $\Delta u = \Delta u_2$ が成り立つ。つまり32bitを全探索すれば $(k_{19}, k_{21})$ が求められる。

ただし、32bitも全探索する必要はなくて、 $k_{19}$ について全探索して、ある $k_{19}$ （の候補）のときの $\Delta u$ の値をキーとする連想配列を用意しておけば、 $k_{21}$ の値を全探索しつつその $\Delta u_2$ について、 $\Delta u$ が同じ値になったときの $k_{19}$ を引っ張ってくる、という中間一致攻撃ができて、これなら16bit全探索が2回で済む。

$(k_{19}, k_{21})$ のペアについては候補が複数組でてくることがあるが、うまくいくケースでは数組に収まるので、それらの組を全部試すか適当に選んだ組が正解であることを祈りながら何度も挑戦すればよいと思って妥協している。

32bit全探索によるk_16, k_17の特定

ここまでで得られた情報をもとに、 $k_{16}, k_{17}$ は全探索して求める。ここまでで4ラウンド目（3.5ラウンド目）の値は一通り逆算できるようになっていて、 $p^{(3)}$ や $q^{(3)}, q'^{(3)}$ が求められるようになっている。これらの値と $k_{16}, k_{17}$ から $t^{(3)}, t'^{(3)}, u^{(3)}, u'^{(3)}$ を求め、 $X^{(4)}_{1} \oplus t^{(3)} = Y^{(3)}_{1}$ と $X'^{(4)}_{1} \oplus t'^{(3)} = Y'^{(3)}_{1}$ が一致するか、 $X^{(4)}_{2} \oplus u^{(3)} = Y^{(2)}_{1}$ と $X'^{(4)}_{2} \oplus u'^{(3)} = Y'^{(2)}_{1}$ が一致するかを複数ケースについて確認すれば正しい $k_{16}, k_{17}$ が求められる。

32bit全探索による暗号鍵の復元

これで、 $k_{16}, k_{17}, k_{18}, k_{19}, k_{20}, k_{21}$ の6個のラウンド鍵がわかり、マスター鍵の16 * 6 = 96bit があきらかになった。残りは32bitなので、全探索すれば良い。単純に鍵の残りの32bitを探索しながら平文を暗号化し、サーバと同じ暗号結果になるようなケースが見つかれば、そのときの鍵が答えになる

コードすべて

以下のgistに貼っておきました。確実性がめちゃめちゃ低いので祈りまくる事になってます。creditの消費量はだいたい1120程度だったようです。

gist.github.com

感想

難しい問題を解けてよかったです。頭がおかしくなるかと思いました。writeupを書くのが大変すぎます。こんな大変な問題を作った@mystizと@deuteriumを尊敬しているし、感謝しているし、うらんでます。一緒に取り組んでくれたkijitoraのメンバーのみなさんと、特にこの問題に一緒に頭を捻ってくれたy011d4さんににも感謝です。

あと、この長いwriteupを最後まで読んでくれた方にも。もし間違っているところや曖昧なことを言ってるところを見つけたら教えて下さい。