Table of Links

Abstract and Intro

Related work

Approaches

Hyperparameter optimization

Estimating the number of novel classes

Full training procedure

Experiments

Conclusion

Declarations

References

Appendix A: Additional result metrics

Appendix B: Hyperparameters

Appendix C: Cluster Validity Indices numerical results

Appendix D: NCD k-means centroids convergence study

4 Hyperparameter optimization

The success of machine learning algorithms (including NCD) can be attributed in part to the high flexibility induced by their hyperparameters. In most cases, a target is available and approaches such as the k-fold Cross-Validation (CV) can be employed to tune the hyperparameters and achieve optimal results. However, in a realistic scenario of Novel Class Discovery, the labels of the novel classes are never available. We must therefore find a way to optimize hyperparameters without ever relying on the labels of the novel classes. In this section, we present a method that leverages the known classes to find hyperparameters applicable to the novel classes. This tuning method is designed specifically for NCD algorithms that require both labeled data (known classes) and unlabeled data (novel classes) during training[1]. This is the case for Projection-based NCD, as described in Section 3.4.

To illustrate, in the split 1 of Figure 4, the model will be trained with the subsets of classes {C2, C3, C4} as known classes and {C0, C1, C5, . . . , C9} as novel classes. It will be evaluated for its performance on the hidden classes {C0, C1} only.

To evaluate a given combination of hyperparameters, this approach is applied to all the splits, and the performance on the hidden classes is averaged. After repeating this process for many combinations, the combination that achieved the best performance is selected. For the final evaluation on the novel classes, in a realistic scenario of NCD their labels are never available. However, in the datasets employed in this article, the novel classes are comprised of pre-defined classes. Therefore, even though these labels

are not employed during training, they can still be used to assess the final performance on the novel classes of different models and compare them against each other.

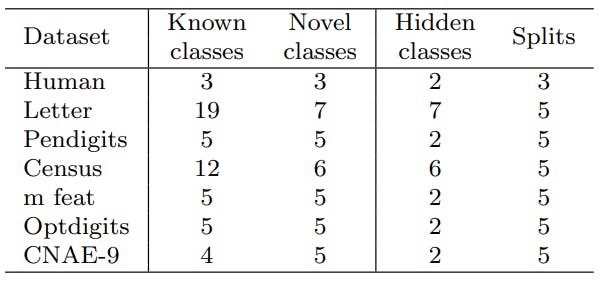
In Table 1, we report for all datasets used in our experiments the number of known classes that are hidden in each split, as well as the number of splits. Note that when the number of known classes is small (e.g. 3 for Human), this approach may be difficult to apply.

Discussion. Similarly to NCD, there are no labels available in unsupervised clustering problems, which makes the task of hyperparameter selection very difficult. To address this issue, clustering algorithms are sometimes tuned using internal metrics that do not rely on labeled data for computation. These metrics offer a means of comparing the results obtained from different clustering approaches. Examples of such metrics include the Silhouette coefficient, Davies-Bouldin index, or Calinski-Harabasz index [33]. However, it is important to note that these metrics make assumptions about the structure of the data and can be biased towards algorithms which make a similar assumption. But unlike unsupervised clustering, the NCD setting provides known classes that are related to the novel classes we are trying to cluster.

[1] To optimize purely unsupervised clustering methods for NCD, we refer the reader to the optimization process of Section 3.3.