从一道CTF题初探NTRU格密码

从一道CTF题初探NTRU格密码
2020-02-06 10:14:39 Author: xz.aliyun.com(查看原文) 阅读量:499 收藏

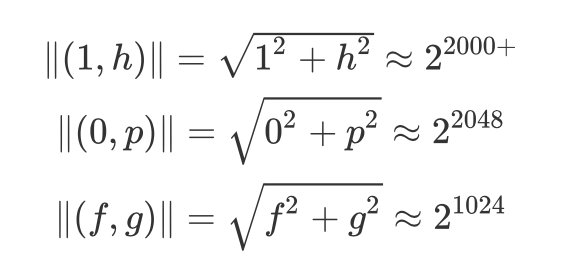
Introduction

巅峰极客线上赛有一道密码题NTURE，是关于非对称密码算法NTRUEncrypt的题目，当时仅有2队解出。

由于知识水平有限，对格相关的密码算法一片空白，所以笔者当时并未解出这道题，但后来一直铭记在心。

赛后虽然有官方wp，并给出了这一题的解法：

不过对于从未接触过格密码的笔者来说，如此简洁的wp显然并没有给予多少帮助。

正好这几天在家有很多空闲时间，便去学习了一番格密码，学到了很多，也总算是把这一题解了出来。

Challenge

题目附件已经上传至网盘：

先贴一下题目的代码：

from Crypto.Util.number import *
import gmpy2
from flag import flag


def generate():
    p = getStrongPrime(2048)
    while True:
        f = getRandomNBitInteger(1024)
        g = getStrongPrime(768)
        h = gmpy2.invert(f, p) * g % p
        return (p, f, g, h)


def encrypt(plaintext, p, h):
    m = bytes_to_long(plaintext)
    r = getRandomNBitInteger(1024)
    c = (r * h + m) % p
    return c


p, f, g, h = generate()
c = encrypt(flag, p, h)
with open("cipher.txt", "w") as f:
    f.write("h = " + str(h) + "\n")
    f.write("p = " + str(p) + "\n")
    f.write("c = " + str(c) + "\n")

在另外一个cipher.txt文件中给出了h, p, c的具体数值。

我们先来审计一下：

generate函数生成了4个参数p, f, g, h，其中，

p: 一个2048-bit的强素数。 (“强”在于p-1和p+1都至少有一个很大的素因数，以防某些攻击)
f：一个1024-bit的随机数。
g：一个768-bit的强素数。
h：

可以视为一个在[0, p)这个区间内随机均匀分布的一个数，基本上2000多bit。

这里要特别留意一下的这四个参数的大小关系，后面会有用到。

encrypt函数对明文（也就是flag）进行了加密：

先生成了一个1024-bit的随机数r
然后加密：

这个加密方式很奇怪，从未遇到过。。。当时解题的时候很懵逼。。

我们再来看看给的参数：h, p, c。

显然，如果我们知道了r，那么就可以直接

解出flag。

但是这里的r是一个随机（本质上是由os.urandom函数）生成的1024-bit数，不可能求得出来的。

如果我们将同余式改写成等式，

我们来估量一下k的范围：

等式右边r：1024-bit，h：2000多bit，m正常来说几百bit，所以r*h + m大概3000多bit。

等式左边c：2000多bit，p：2000多bit。

因此k大概也有1000多bit，从k出发也无法求解。

况且非对称密码，本来就是需要使用一些数学上巧妙的变换来解密的，并非简简单单地暴力破解就能解决的。

所以想要求解，只能在剩下的两个未知参数f, g上作文章了。

What if

假设一下，如果我们知道了f, g，会怎么样？

我们来做一些代数变换：

这是我们目前已知的两个模p的关系式，我们将上式代入下式，这样就能消去h：

现在假设我们已经知道了f, g，那么只有r, m未知；还是需要知道r才能解出m。

不过我们在式子两边同时乘上f来试试看：

看上去似乎并没有好一些？？不过这个时候，我们再来认真观察一下式子右边的内容：

r：1024-bit
g：768-bit
m：flag字符串转成数字，一个字符8bit，一般来说flag不会太长，所以基本上是小于1000bit的。
f：1024-bit
p：2048-bit

有没有发现什么？？？

没错，式子右边的内容

这意味着，式子右边根本就没有被mod p，是完完整整的r*g + m*f！！！

也就是说，如果我们令

即使c*f是肯定会大于p的，但是mod p后的结果，就是完完整整的r*g + m*f。

即，

这里很关键，一定要弄明白！

也就是说，我们通过一些数学上的变换以及参数之间巧妙的大小关系，成功地在同余式里面找出了一个等式！

可是这又有什么用呢？

这就足以让我们能直接绕过r，算出m。

对该等式取模g，

这样，r*g这一项就直接消失了。

其中，a, f, g均已知，求m就很轻松了：

注意：

这里是在mod g下运算，还记得g是一个768-bit的强素数么？这就保证了，虽然f是个1024-bit的数，但是在mod g下，f' = f - k*g的逆元必定存在。

此处的f^-1与h = f^-1 * g (mod p)里的不是同一个东西。

g有768-bit，768/8=96，flag字符串一般来说不会超过96个字符长，因此m比g小，所以最终算出来的就是完完整整m。

TL;DR

如果我们能够知道f, g，那么我们就能解密：

# sage

# Known: h, p, c, f, g
a = (c*f % p) % g
m = a*inverse_mod(f, g) % g
print(hex(m).decode('hex'))

Underlying

好了，只要我们能求出f, g，就能解密。

而我们唯一知道的关于f, g的关系式只有，

我们如何从中求出f, g呢？

这里就是格（Lattice）的范畴了。

先简单介绍一下lattice。

大家应该都学过线性代数。

如果想温习一遍，推荐3b1b的Essence of linear algebra。

给定一组线性无关的基向量（basis）v1, v2, ..., vn，那么这些基向量的所有线性组合(linear combinations)

所形成的集合，就叫做这组基向量所张成的空间(span)。

例如，在二维平面中，如果我们选取两个单位正交向量作为基向量

那么由这两组基向量的所有可能的线性组合

张成的空间就是整个二维平面。

反过来，这个二维平面上的任何一点，都可以由这两组基底的一个线性组合来表示：

ok，其实lattice的定义跟这个差不多。

给定一组线性无关的基向量v1, v2, ..., vn，那么这些基向量的所有整系数线性组合

所形成的集合，就叫做这组基向量所张成的格(lattice)。

系数不再是任何实数，变成了是任何整数

也就是说，从无数个连续的点变成了无数个离散的点。

不同的基底，可能会张成不同的lattice：

对原基底进行整系数线性转换得到的新的基底，张成的lattice仍旧不变：

其中，

注意：同一个lattice有很多组基底。

在lattice里面，有两个知名的难题：

SVP(最短向量问题，Shortest Vector Problem)：给定lattice和基向量，找到lattice中的一个长度最短的非零向量。
CVP(最近向量问题，Closest Vector Problem)：给定lattice和基向量，以及一个不在lattice上的目标向量，找到lattice中一个距离目标向量最近的格向量。

在广义上的这两大难题已经被证明是NP-hard。

这一题实质上就是一道求解SVP的题目。

虽说，SVP是NP-hard的，但是本题的lattice维度很低，只有2维，所以还是很容易求解的。

实际上，LLL算法及其变种算法是目前已知在较低维度的lattice中求解SVP的最好的算法，但是在较高维度中就比较乏力。

所以，并不是说NP-hard就不可能求解。

那么，如何将本题看作成一个lattice中求解SVP的题目呢？

针对

也就是

我们可以构造一个由下面这个矩阵M中的两个行向量(1,h), (0,p)所张成的lattice：

下面我们来证明向量(f, g)是在这个lattice上的。

Proof：

我们可以将同余式

改写成等式

将u*p移至左边，

我们可以发现

向量(f,g)可以由两组基向量M的某种整系数线性组合(f, -u)来表示，因此向量(f,g)就在这个lattice上。

Q.E.D.

我们再来看看h, p, f, g的大小。

h：2000多bit
p：2048-bit
f：1024-bit
g：768-bit

相对于两个基底向量(1, h), (0, p)来说，向量(f, g)的长度要小得多得多：

根据Gaussian heurstic可知，在这个lattice中最短向量的长度大概在sqrt(2^2048)=2^1024左右。因此，很大概率上，这个(f, g)就是这个lattice的最短向量。

可见，一开始参数的大小设置，是很关键的一点。

那么如何在lattice里求最短向量呢？

在2维里，早在200年前，高斯（Gauss）就发现了一个能稳定求解的算法（Gauss Lattice Reduction）。

令L是由两个基向量v1, v2所张成的2维lattice，假定|v1| < |v2|，我们现在通过减去v1的某个倍数来使得v2变短。

这样我们就能够得到一个与v1正交（垂直）的新向量v2*，且使得v2变短了（且是通过这种方式能变的最短的情况）。

但是，现在我们在lattice里面，不能减去任意倍数的v1，只能减去整数倍的v1。

所以，我们能做的就是，减去整数倍的v1且尽量使得v2变得最短：

减完，如果v1 > v2，那么交换v1, v2，继续；否则，就结束。

这个算法很容易实现：

# sage
def GaussLatticeReduction(v1, v2):
    while True:
        if v2.norm() < v1.norm():
            v1, v2 = v2, v1
        m = round( v1*v2 / v1.norm()^2 )
        if m == 0:
            return (v1, v2)
        v2 = v2 - m*v1

例如，对于由v1 = (66586820,65354729), v2 = (6513996,6393464)张成的lattice使用上述算法：

(66586820, 65354729), (6513996, 6393464)

(6513996, 6393464), (1446860, 1420089)

(1446860, 1420089), (-720304, -706981)

(-720304, -706981), (6252, 6127)

(6252, 6127), (-1324, -2376)

(-1324, -2376), (2280, -1001)

(2280, -1001), (-1324, -2376)

因此在这个lattice中，最短向量即为(2280, -1001)。

再回到这一题中，我们使用这个算法来求解M中的最短向量：

# sage

# h = ...
# p = ...
v1 = vector(ZZ, [1, h])
v2 = vector(ZZ, [0, p])
print GaussLatticeReduction(v1, v2)[0]

大概在20s后能得到结果：

(140165891500972861127767415311334757297477816480570735901532575717579672765221212171489392644327018202900088035383969034846193847149851961591661082906530495738734185460636601059708032788268225305120040067251226533612047405603785333261269570827395533567542600084996230099530440207162530350599289132101020447759, 1493239469420336600577802657161324795848374750185055876743560582622232360193779109171117333425338766341860983348309692998243289015442909620365263900067613009409717218816514258676437322125744209790095123709189541828478158286030084857)

经过检验，发现140165...759的确为1024bit，149323...857的确为768bit的质数。

即，求得的结果就是(f, g)。

TL;DR

(f, g)就是一个在特定的2维lattice上的最短向量，使用GaussLatticeReduction或者LLL算法即可解出。

Exploit

好了，现在万事俱备，就差最终exp了。

# sage

def GaussLatticeReduction(v1, v2):
    while True:
        if v2.norm() < v1.norm():
            v1, v2 = v2, v1
        m = round( v1*v2 / v1.norm()^2 )
        if m == 0:
            return (v1, v2)
        v2 = v2 - m*v1

h = 7257231567493321493497732423756001924698993879741072696808433246581786362611889417289029671240997843541696187487722285762633068287623369923457879458577466240950224087015909821079480431797917376609839097610864517760515986973340148901898582075413756737310797402537478388864632901178463429574227279668004092519322204990617969134092793157225082977967228366838748193084097651575835471869030934527383379794480007872562067799484905159381690179011192017159985260435844246766711550315143517066359521598424992244464723490166447105679062078049379153154659732304112563255058750656946353654402824529058734270363154894216317570784
p = 23969137365202547728693945383611572667294904799854243194734466236017441545927679469239814785947383727854265554138290421827510545078908517696536495567625593439996528098119344504866817224169113920532528233185011693829122447604993468817512696036673804626830507903206709121383065701222707251053362179946170981868061834734684494881504724254812067180384269711822738708203454131838741703416329765575995359232573740932069147491776326045743679105041246906081872936901848272288949389026129761726749334006319072981386763830897454245553866145620689939497868469730297795063648030738668273210516497399954626983672357236110363894081
c = 6388077150013017095358415295704360631706672647932184267739118115740221804173068089559645506533240372483689997499821300861865955720630884024099415936433339512125910973936154713306915269365877588850574948033131161679256849814325373882706559635563285860782658950169507940368219930971600522754831612134153314448445006958300840618894359885321144158064446236744722180819829183828290798747455324761671198097712539900569386477647697973195787663298318786718012522378981137877863153067057280649127202971806609339007027052518049995341356359016898069863799529357397514218249272201695539181908803360181347114492616706419618151757

# Construct lattice.
v1 = vector(ZZ, [1, h])
v2 = vector(ZZ, [0, p])
m = matrix([v1,v2]);

# Solve SVP.
v1 = vector(ZZ, [1, h])
v2 = vector(ZZ, [0, p])
m = matrix([v1,v2]);
shortest_vector = m.LLL()[0]
# shortest_vector = GaussLatticeReduction(v1, v2)[0]
f, g = shortest_vector
print(f, g)

# Decrypt.
a = f*c % p % g
m = a * inverse_mod(f, g) % g
print(hex(m).decode('hex'))

# flag{c3bb1f88-2c0b-48fc-9902-beada6d50df6}

事实上，sagemath中自带LLL算法的实现，比我们的这个自制GaussLatticeReduction（大概20s）要快上很多（不到1s）。

Summary

CTF密码题中，RSA是出现次数最多的非对称密码算法，而基于DLP的ElGamal和ECC以及一些基于格中难题的密码算法却很少出现。因此，适当地扩展自己的知识面还是很有必要的。

由于篇幅原因，未能阐释NTRUEncrypt非对称加密算法在高维度中的实现（可能需要具备一定的的数学基础才能理解）以及LLL算法，在最后只能给出一些链接供感兴趣的师傅深入学习了：

An Introduction to Mathematical Cryptography Section 7.9. - 7.14.
NTRUEncrypt wiki
Building Lattice Reduction (LLL) Intuition
Mathematics of Public Key Cryptography Section 17

文章来源: http://xz.aliyun.com/t/7163
如有侵权请联系:admin#unsafe.sh