前言

同RSA（Ron Rivest，Adi Shamir，Len Adleman三位天才的名字）一样，ECC（Elliptic Curves Cryptography，椭圆曲线密码编码学）也属于公开密钥算法。RSA算法是基于大整数因子分解问题（IFP），ECC算法是基于椭圆曲线上离散对数计算问题（ECDLP）。

ECC加密算法

1.从椭圆曲线说起

要想理解ECC，那么椭圆曲线一定是一个不能回避的问题。不过请放心，并不需要了解很多，够用即可，甚至很多细节也都不用深究。椭圆曲线其实是一类曲线，而且并不像其名字所说的那样，它和我们高中所学的椭圆公式并不一样。

一条椭圆曲线是在射影平面上满足方程 Y^2^Z+a~1~XYZ+a~3~YZ^2^=X^3^+a~2~X^2^Z+a~4~XZ^2^+a~6~Z^3^所有点的集合，且曲线上的每个点都是非奇异（或光滑）的。

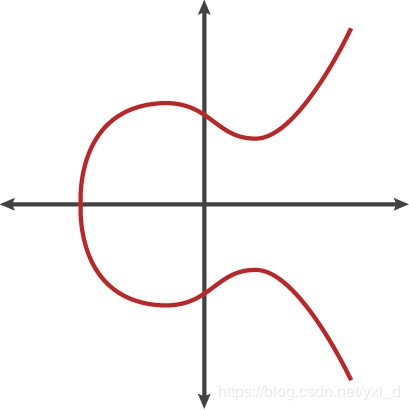
是不是看着像天书？确实是的，因为我其实并没有介绍里面的名词比如射影平面，因为我们不需要了解那么多，因为并不是所有的椭圆曲线都适用与加解密。在密码学中，也只用到椭圆曲线的子集如y^2^=x^3^+ax+b，这是最简单的一种，而且我们使用高中数学也能明白其图像长什么样子。
其图像如下所示：

从上图中，我们可以看到，这条曲线关于x轴对称（但是要注意，这只是一类特殊的椭圆曲线），并且每一点都有切线。下面就基于这一类椭圆曲线描述一系列定义和性质。

首先，我们还需要定义一些小小的特殊成分，正如同在小学数学中我们有零，在初中数学平面直角坐标系中我们有原点一样，我们这里也有一个特殊的点无穷远点 O∞并称为零元，你可以顾名思义想象它在哪里，显然我们画不出来，但是想象不出来也没关系（虚数i大家也难以想象出来吧），我们只需要会运算就可以。
接着需要基于这个曲线定义一些运算，最重要的无疑是加法，而基于加法我们可以衍生出减法和乘法。

首先是加法， 对于平面上两点P和Q，我们可以这么定义其和R以及和对应的负值 -R（我们称之为负元）。

而如果 P和Q是同一点，那么直线PQ就是在该点的切线（回想一下之前所讲的任何一点切线都存在），那么和也就同样可以得到，并且通过这样的方式，我们可以将和拓展到2P、3P......nP，因此我们也定义出了乘法，而-R的存在也使得我们可以定义减法。

好了，在上面，我们定义了加法减法和乘法，当然，尽管我们没有定义除法，但很容易想到除法可以反过来由乘法推算出。确实如此，我们小学中除法也是这么来的。但是在这里，除法并没有什么除法法则帮我们计算，因此除法远比乘法难以计算。

对于ECC，我们对椭圆曲线的知识背景了解就只需要这么多就可以了。

2.有限域上的椭圆曲线

有限域是什么呢？简单地说，就是我们从一个集合中选一个子集，那么这就构成了一个有限域。那么为什么我们在这里需要有限域呢？这个问题不难回答，椭圆曲线的点是属于实数的，而计算机并没有办法包含所有的实数的，甚至于很多简单的小数都没办法包含，因此，我们需要限制一个在有限域内的椭圆曲线。
因此，我们可以定义以下的有限域F~p~，其只包含有限个取值。

• p为素数，而有限域F~p~中也只包含 p个元素分别是0,1,2,3......p-2,p-1。
• F~p~内的加法法则是a+b≡c(mod p)，可以简单的认为是将和对p取模以使得结果映射到有限域内。
• F~p~内的乘法法则是a×b≡c(mod p)。
• F~p~内的除法法则是a/b≡c(mod p)，即a×b^-1^≡c (mod p)，其中b^-1^也是一个0到p-1之间的整数，但满足b×b^-1^≡1(mod p)

因此，我们可以定义如下在有限域F~p~上的的椭圆曲线如下所示。
有方程y^2^=(x^3^+ax+b)(mod p)，其中4a3+27b2≠0　(mod p)，所有满足上述方程的有限域内的点(x,y)并加上O∞无穷远点构成了E~p~(a,b)。

我们以y^2^=x^3^+x+1 (mod 23)为例，其在有限域上的的椭圆曲线图像如下所示：

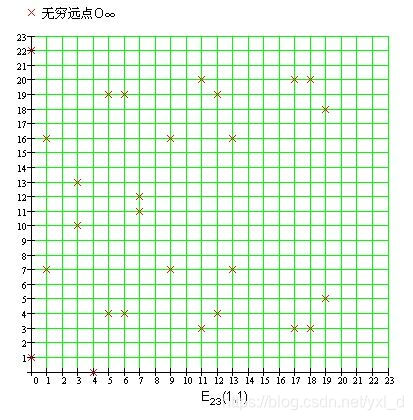
可见，我们现在所看见的只有一系列离散的点。
在有限域上的椭圆曲线自然也是有其加法的，但是已经不是几何意义上的加法了，在这里直接给出结论，因为这其实已经不需要过于深究了。

• 无穷远点 O∞是零元，有O∞+ O∞= O∞，O∞+P=P
• P(x,y)的负元是 (x,-y)，有P+(-P)= O∞
• P(x~1~,y~1~),Q(x~2~,y~2~)的和R(x~3~,y~3~) 有如下关系：
  x~3~≡k^2^-x~1~-x~2~(mod p)
  y~3~≡k(x~1~-x~3~)-y~1~(mod p)
  其中若P=Q 则 k=(3x^2^+a)/2y~1~ 若P≠Q，则k=(y~2~-y~1~)/(x~2~-x~1~)

最后，我们讲一下椭圆曲线上的点的阶。对于椭圆曲线上一点P，若存在最小的正整数n，使得nP=O∞，则称n为P的阶。若不存在这样的n，我们则称P是无限阶的。但是幸运的是，对于有限域上的的所有点都是有阶的。

3.ECC自我理解

大体上是说，给出一个曲线：y^2=x^3+ax+b，
确定下来a和b，然后找一个在曲线上的点G（x1,y1），
然后自己随机生成一个k（私钥），
然后生成公钥K=kG，
注意:这里的kG可不是k*G这么简单，这是几何意义上的：

• K=G+G+G+G+……+G（k个G）

然后把公钥给出去，私钥留给自己。
和RSA差不多，重点应该是在于如何求K。

• G（x1,y1）,P（x2,y2）

核心公式：

x3≡t^2-x1-x2(mod p)
y3≡t(x1-x3)-y1(mod p)
其中
若P=G 则 t=(3x^2+a)/2y1 
若P≠G 则 t=(y2-y1)/(x2-x1)

ECC题目练习

看一下题目介绍

参照大佬写的求公钥脚本

a=16546484
p=15424654874903
def egcd(t, b):
    if t == 0:
      return (b, 0, 1)
    else:
      g, y, x = egcd(b % t, t)
      return (g, x - (b // t) * y, y)

def modinv(o, m):
    g, x, y = egcd(o, m)
    if g != 1:
      raise Exception('modular inverse does not exist')
    else:
      return x % m

def ecc_m(x1,y1,x2,y2):
    if ((x1 == x2) & (y1 == y2)):
        fenzi=3*x1*x1+a
        fenmu=2*y1
    else:
        fenzi = y2 - y1
        fenmu = x2 - x1
    m=(abs(fenzi) * modinv(abs(fenmu), p)) % p
    if ((fenzi >= 0 & fenmu >= 0) | (fenzi < 0 & fenmu < 0)):
        return m
    else:
        return p - m

def ecc_x(x1,x2,m):
    result_x = m*m-x1-x2
    if result_x>0:
        return result_x%p
    else:
        p1=p
        if abs(result_x)>p1:
            shang=abs(result_x)/p
            p1=shang*p+p
        return p1+result_x

def ecc_y(x1,result_x,y1,m):
    result_y = m*(x1-result_x)-y1
    if result_y>0:
        return result_y%p
    else:
        p1 = p
        if abs(result_y) > p1:
            shang = abs(result_y) / p
            p1 = shang * p + p
        return p1 + result_y

def ecc_result_x(x1,y1,x2,y2):
    m = ecc_m(x1,y1,x2,y2)
    result_x=ecc_x(x1,x2,m)
    return result_x

def ecc_result_y(x1,y1,x2,y2):
    m = ecc_m(x1,y1,x2,y2)
    result_x = ecc_x(x1, x2, m)
    result_y=ecc_y(x1, result_x, y1, m)
    return result_y

x1=x2=x3=6478678675
y1=y2=5636379357093
n=546767
while(n>0):
    x2=ecc_result_x(x1,y1,x2,y2)
    y2=ecc_result_y(x1,y1,x3,y2)
    x3=x2
    n-=1
print x2,y2
result = x2+y2
flag = "XUSTCTF{%s}"%result
print(flag)

运行后即可得到flag

后记

个人认为ECC椭圆加密算法的难点关键还是在于中间涉及到数论的知识，本人较菜，还需学习。