用SageMath实现RSA低指数攻击

用SageMath实现RSA低指数攻击
2019-11-27 10:35:03 Author: xz.aliyun.com(查看原文) 阅读量:407 收藏

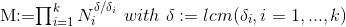
参考论文

《Low-Exponent RSA with Related Messages 》by Coppersmith, Franklin, Patarin and Reiter
《Solving Systems of Modular Equations in OneVariable: How Many RSA-Encrypted MessagesDoes Eve Need to Know?》by Alexander May, Maike Ritzenhofent

介绍低指数相关攻击，主要是翻译文章并使用SageMath复现攻击。

使用工具：

python2，依赖库：gmpy2
SageMath

主要讨论有相关关系的消息进行RSA加密的情况。多次RSA加密如果涉及到的模数 Ni 不全部互质，那就可以直接求出其最大公约数作为模数的一个因子，分解模数进而完成解密。

如果消息不进行填充就重复加密，是比较容易攻击的。

比如G. Simmons提出的共模攻击。一段消息m被加密两次。N相同，但是两次加密使用的 e 互质。用拓展欧几里得算法可以得到直接计算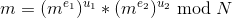完成攻击。所以我们只讨论带填充的加密情况。

我们接下来讨论的都是认为以下条件成立的情况下进行的：

公钥已知
模数互质，且分解模数困难
明文经过填充
所有密文已知

RSA原理参考自https://ctf-wiki.github.io/ctf-wiki/crypto/asymmetric/rsa/rsa_theory-zh/

随机选择两个不同的大质数 p 和 q，计算 N = p×q
根据欧拉函数，求得 φ(N)=φ(p)φ(q)=(p−1)(q−1)
选择一个小于 φ(N)的整数 e，使 e 和 φ(N) 互质。并求得 e 关于 φ(N) 的模反元素，命名为 d，有
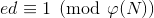
将 p和 q 的记录销毁

此时，(N,e)是公钥，(N,d)是私钥。设加密函数为E，解密函数为D

功能：在多项式时间内求解一元首一多项式 f(x)所有的根

条件：

如果X 为根 x 的上限

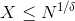
可求出一元方程
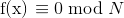的所有根 x0 。

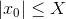
费时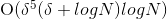

sage实现

from sage import *
PR = PolynomialRing(ZZ, 'x')
x = PR.gen()
FF = (x+1024)^10 + 23*x
m = FF.small_roots(X=2**760, beta=7./8) #一个列表，表示所有根

参考：《Low-Exponent RSA with Related Messages 》by Coppersmith, Franklin, Patarin and Reiter。

讨论带线性填充和非线性填充的共模攻击思路。

攻击情景：

k个明文满足某个δ阶多项式P(即所有明文存在某种相关关系)。

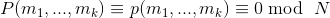
使用相同RSA公钥（e, N）加密得到 k 个密文

可以在时间复杂度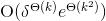内恢复所有明文。

也就是说得知 k+1 个多项式就可能解出所有明文。

推广 e

我们先讨论简单情况，再证明 e 很大的时候也是可解的。

k = 2,只涉及两组消息。

δ = 1 ，即明文可以如下表示

为了方便我们讨论如下情况

e=3

加密两次，得到如下结果：

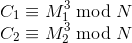
可以转化成一元一次方程，求解明文(以下除法为乘逆元)：

e=5

容易找到多项式P(x) 和 Q(x)，满足以下关系求得x。

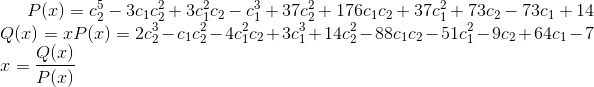
事实上, e 很大的时候我们也能求出多项式的最大公约式得到线性多项式 x - m 以求解明文。

证明

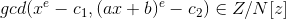
从而计算得到 x 再由明文和x的多项式f(x)即可得到所有明文。

推广 δ > 1

如果所有的明文都可以用某个 δ 阶一元多项式 f 表示，δ > 1。现在证明此时也是可解的。

如果两个明文和 x 之间的关系是非线性的，加密后有如下关系

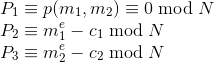
在知道填充方式的前提下，可以求解所有明文。

证明：

令 x, y 分别代表 m1，和 m2。
在 Z/N 环上，计算 P1(x, y) 和P2(x)的关于 x 的结式，也就得到一个在 y 上的δe 阶多项式 P4。
计算 P4 和 P3 的最大公约式，也就是线性多项式 y-m2，m2可以用该线性多项式表达。
将m2（此时仍未求解）代入P1，得到一个只关于 x 的多项式，再求解此多项式和 P2的最大公约式，就能得到x=m1。

证毕, δ > 1 也可以求解。

推广 k>2

当存在多组消息后，k个消息的相关于多项式 P，但是多项式 P 可能是一个包含多个元的。下面证明k>2也是可解的。

k个消息满足多项式P，共有k个多项式如下：

接着可以求出Groebner基，称为向量B，则

求得所有明文。

复杂度

我们将在文章后面使用sage计算Groebner基，进而得到所有明文。

k=2小结

无论填充是线性的还是非线性的，如果所有明文 x 都满足多项式P，转化成方程如下

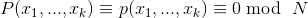
使用相同公钥加密后，只要再得到两段密文，可以在复杂度

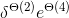
求出Groebner基后，求解一元e次方程组得到的根即为所求。
举例：

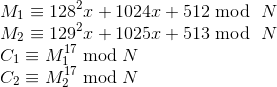
题目如下：

import gmpy2
import random
p = gmpy2.next_prime(random.getrandbits(1024))
q = gmpy2.next_prime(random.getrandbits(1024))
assert(p != q)
n = p * q
e = 17
m = int('Flag{123123-1231-13123213-123123}'.encode('hex'), 16)
cnt = 2
A = [(i + 128)**2 for i in range(cnt)]
B = [(i + 1024) for i in range(cnt)]
C = [(i + 512) for i in range(cnt)]
Cs = [int(pow(A[i] * m**2 + B[i]*m + C[i], e, n)) for i in range(cnt)]
print 'N=', n
print 'e=', e
print 'Cs=', Cs

SageMath 解题脚本如下：

from sage import *
# 事先需要将公钥密文添加到sage脚本中
N=....
e= 17
Cs= [...,...] # len(Cs) == 2
cnt = 2

A = [(i + 128)**2 for i in range(cnt)]
B = [(i + 1024) for i in range(cnt)]
C = [(i + 512) for i in range(cnt)]

PR = PolynomialRing(Zmod(N), 'x', 1)
x = PR.gen()
Fs = [((A[i] * x**2 + B[i]*x + C[i])**e - Cs[i]) for i in range(cnt)]
I = Ideal(Fs)
G_b = I.groebner_basis()[0]
m = ZZ(-G_b(0))
m = int(m + B[0])
print hex(m)[2:].strip('L').decode('hex')

k > 2总结

和k=2的情形不同之处在于此时可以涉及多个未知数。

k个明文相关，相关多项式共有k个元，已知k+1个以上关于k个明文的多项式。

示例

已知如下条件

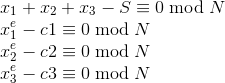
# 参考2019redhat ctf 的密码学题目relate
import gmpy2
import random
p = gmpy2.next_prime(random.getrandbits(1024))
q = gmpy2.next_prime(random.getrandbits(1024))
assert(p != q)
n = p * q
phin = (p-1)*(q-1)
e = 5
d = gmpy2.invert(e, phin)
assert(e*d % phin)
def pad(msg, length):
    l = len(msg)
    return msg + chr(length - l) * (length - l)
flag = 'Flag{123123-1231-13123213-123123}'
flag = pad(flag, 48)
m = [int(flag[i * 16:i * 16 + 16].encode('hex'), 16) for i in range(3)]
print 'S=', sum(m) % n
cnt = len(m)
A = [(i + 128)**2 for i in range(cnt)]
B = [(i + 1024) for i in range(cnt)]
C = [(i + 512) for i in range(cnt)]
Cs = [int(pow((A[i] * m[i]**2 + B[i] * m[i] + C[i]), e, n)) for i in range(cnt)]
# Cs = [int(pow((B[i] * m[i] + C[i]), e, n)) for i in range(cnt)]
print 'N=', n
print 'e=', e
print 'Cs=', Cs

求解Groebner 基即可

sage解法

# 事先将题目的输出填入对应参数位置
# coding:utf-8
from sage import *

S= 
N=
e= 5
Cs= []
cnt = 3
A = [(i + 128)**2 for i in range(cnt)]
B = [(i + 1024) for i in range(cnt)]
C = [(i + 512) for i in range(cnt)]

PR = PolynomialRing(Zmod(N), 'x', cnt)
x = PR.gens()  # 生成 cnt 个x，用下标区分符号
Fs = [((A[i] * x[i]**2 + B[i] * x[i] + C[i])**e - Cs[i]) for i in range(cnt)]
Fs.append(x[0] + x[1] + x[2] - S)
I = Ideal(Fs)
G_b = I.groebner_basis()
for b in G_b[:-1]:
    mi = ZZ(-b(0, 0, 0))  # 3 个元
    mi = hex(mi)[2:].strip('L')
    print (('', '0')[len(mi) %2]+mi).decode('hex')

讨论使用多组不同的RSA公钥进行加密的攻击手段。

如果使用到的模数不全部互质数，则可以直接求出最大公约数分解模数完成解密。接下来我们讨论的都是模数全部相互互质的情况。

Håstad问题

描述：

使用不同的互质模数，相同的参数 e，加密 e 个明文，得到 e 个密文。这 e 个明文都是关于x的线性填充结果，即

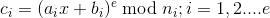
求解：

可以得到e 个方程

因为这 e 个模数都是互质的，那么可以由中国剩余定理得到一个多项式，此多项式必定有唯一解。

又因为此多项式满足LLL算法约束，则可以求解出所有根，得到 x ，进而恢复明文。

举例

e=5

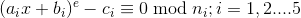
因为5个模数相互互质，所以使用中国剩余定理得到一个5阶多项式，满足LLL算法条件，可求解。

#　题目脚本
import gmpy2
import random
m = int('Flag{123123-1231-13123213-123123}'.encode('hex'), 16)
e= 5
cnt = e
A = [(i + 128) for i in range(cnt)]
B = [(i + 1024) for i in range(cnt)]
Cs = []
Ns = []
ds = []
for i in range(cnt):
    while True:
        p = gmpy2.next_prime(random.getrandbits(1024))
        q = gmpy2.next_prime(random.getrandbits(1024))
        N = p * q
        phin = (p - 1) * (q - 1)
        try:
            d = gmpy2.invert(e, phin)
        except:
            continue
        if (e * d % phin == 1):
            break
    Ns.append(int(N))
    c = pow(A[i] * m + B[i], e, N)
    Cs.append(c)
    ds.append(d)
    del p, q,d
for i in range(cnt):
    assert(pow(Cs[i], ds[i], Ns[i]) == A[i] * m + B[i])

print 'Cs = ', [int(item) for item in Cs]
print 'Ns = ', [int(item) for item in Ns]
print 'A= ', A
print 'B=', B
print 'e=', e

sageMath 解题脚本

# coding:utf-8
from sage import *

Cs = []
Ns =  []
A=  [128, 129, 130, 131, 132]
B= [1024, 1025, 1026, 1027, 1028]
e= 5

# solve
cnt = e
PR = PolynomialRing(ZZ, 'x') #１个元
x = PR.gen()
Fs = []
for i in range(cnt):
    f =  PR( (A[i]*x + B[i])**e - Cs[i] )　# 五个式子
    ff = f.change_ring(Zmod(Ns[i]))
    ff = ff.monic()
    f = ff.change_ring(ZZ)
    Fs.append(f)

F = crt(Fs, Ns)
M = reduce( lambda x, y: x * y, Ns )
FF = F.change_ring(Zmod(M))
m = FF.small_roots()#ＬＬＬ算法
if m:
    m = hex(int(m[0]))[2:].strip('L')
    print(['', '0'][len(m) % 2] + m).decode('hex')
else:
    print 'no ans'

SMUPE-问题

参考《Solving Systems of Modular Equations in OneVariable: How Many RSA-Encrypted MessagesDoes Eve Need to Know?》by Alexander May, Maike Ritzenhofent

SMUPE定义

SMUPE问题： a system of univariate polynomial equations problem = 一元多项式方程组求解问题

k 是一个整数，N为满足RSA算法的模数，δ是多项式的阶。有

多项式方程组表示如下, 目的是求解 x

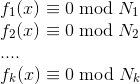
求解条件

Alexander May, Maike Ritzenhofent提出一种求解方法，简单地说当多项式的阶 δ 满足以下情况时可解. δ是多项式的阶

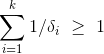
具体描述：

令
作为 SMUPE-问题的首一多项式组

定义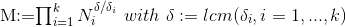

SMUPE-问题则 the SMUPE-problem 可以在以下复杂度解决。

攻击算法

先给出一个简单的例子，在后面会给出这种情况下的攻击脚本：

将一个明文m进行填充，分别使用4组RSA公钥进行加密(模数互质)，多项式(1)描述如下

公钥分别是 (3, N0) ，(3, N1)，(5, N2)， (5, N3)

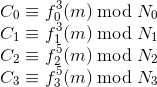
进行如下转化，使得每个方程左边都是6阶的

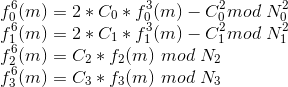
移项，令方程左边为0

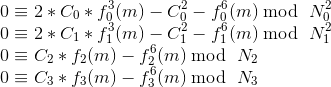
4个模数互质，且有四个同余式，则可以用中国剩余定理求解，得到关于m的一元6阶多项式。

如果m满足LLL算法，

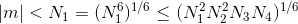
可以求解得到多项式的根 m

证明

设 $x_0$ 作为多项式(1)的一个解。则$x_0$为以下方程组的解

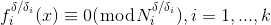
所以方程都是首一δ 阶多项式。

使用中国剩余定理求解方程组得到一个**首一 δ 阶多项式 f(x) ，且x0 是下式的根。
\equiv 0 \bmod M,M:=\prod ^k_{i=1}N_i^{\delta /\delta _i} $)
因为 f(x) 每一项 x^δ 的系数aδ 存在如下关系
![图片.png](https://latex.codecogs.com/gif.latex?%24%24%20a%5Cdelta%5Cequiv%201%20%28%5Cbmod%20N_i%5E%7B%5Cdelta/%5Cdeltai%7D%29%2Ci%3D%201%2C%20.%20.%20.%20%2C%20k%20%24%24)
所以有
![图片.png](https://latex.codecogs.com/gif.latex?%24%24%20a%5Cdelta%20%5Cequiv%201%20%5Cbmod%20M%2Ci%3D%201%2C%20.%20.%20.%20%2C%20k%20%24%24)
中国剩余定理可以在时间复杂度

完成。

当$(x) 的根 x0 满足

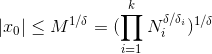
可以使用LLL算法求解 x0 ， LLL算法时间复杂度为

所以整个攻击的时间复杂度为 $O(\delta ^6log_2M)$

例题

参考 2019 redhat CTF 密码学题目《精明的Alice》

是文章在上面给出的SMUPE简单例子

import gmpy2
import random

def RSA(e):
    while True:
        p = gmpy2.next_prime(random.getrandbits(1024))
        q = gmpy2.next_prime(random.getrandbits(1024))
        N = p * q
        phin = (p - 1) * (q - 1)
        try:
            d = gmpy2.invert(e, phin)
        except:
            continue
        if (e * d % phin == 1):
            break
    return e, int(N)
PKs = [RSA(3), RSA(3), RSA(5), RSA(5)]
m = int('Flag{123123-1231-13123213-123123}'.encode('hex'), 16)
cnt = 4
A = [(i + 128) for i in range(cnt)]
B = [(i + 1024) for i in range(cnt)]
Cs = [pow(A[i] * m + B[i], PKs[i][0], PKs[i][1]) for i in range(cnt)]
print 'Cs = ', [int(item) for item in Cs]
print 'PKs = ', PKs
print '[+] enc complited.'

SageMath 脚本

# 将题目输出填入对应变量
from sage import *
Cs = [...]
PKs =  [(3,..), (3,..), (5,..), (5,..)]
cnt = 4
A = [(i + 128) for i in range(cnt)]
B = [(i + 1024) for i in range(cnt)]
PR = PolynomialRing(ZZ, 'x')
x = PR.gen()

Fs = []
for i in range(cnt):
    f =  PR( ( A[i]*x + B[i] )**PKs[i][0] - Cs[i] )
    ff = f.change_ring( Zmod(PKs[i][1]) )
    ff = ff.monic()
    f = ff.change_ring(ZZ)
    Fs.append(f)
F = crt( [ Fs[0]**2, Fs[1]**2, x*Fs[2], x*Fs[3] ], [ PKs[i][1] for i in range(cnt) ] )

M = reduce( lambda x, y: x * y, [ PKs[i][1] for i in range(cnt) ] )
FF = F.change_ring( Zmod(M) )
m = FF.small_roots(X=2**760, beta=7./8)[0]
m = hex(int(m))[2:].strip('L')
print (('', '0')[len(m) % 2]+m).decode('hex')

为了方便复现，使用的工具已经尽可能地少（其实sage和python已经足够了）

SageMath安装教程：http://doc.sagemath.org/html/en/tutorial/introduction.html#installation

笔者的理论水平有限，纰漏之处还请读者海涵。

Reference：

《Low-Exponent RSA with Related Messages 》by Coppersmith, Franklin, Patarin and Reiter
《Solving Systems of Modular Equations in OneVariable: How Many RSA-Encrypted MessagesDoes Eve Need to Know?》by Alexander May, Maike Ritzenhofent
RedHat CTF 官方writeup ：https://mp.weixin.qq.com/s/MKaMMihP8gPSYKswAxjNqQ
CTFWiki：https://ctf-wiki.github.io/ctf-wiki/crypto/
SageMath文档：http://doc.sagemath.org/html/en/tutorial/introduction.html

文章来源: http://xz.aliyun.com/t/6813
如有侵权请联系:admin#unsafe.sh