每周文章分享

2023.06.05-2023.06.11

标题: A Novel Hybrid Particle Swarm Optimization Algorithm for Path Planning of UAVs

期刊: IEEE INTERNET OF THINGS JOURNAL, VOL. 9, NO. 22, 15 NOVEMBER 2022

作者: Zhenhua Yu, Zhijie Si, Xiaobo Li,  Dan Wang, and Houbing Song.

分享人: 河海大学——祝远波

研究背景

无人驾驶飞行器（Unmanned Aerial Vehicles，UAVs）在各个领域都变得越来越重要，包括侦察、救援和军事行动等。尽管有各种优化算法可用于无人机路径规划，但它们在处理复杂的三维环境的能力方面仍有局限。为了解决这个问题，本文提出了一种新型的混合粒子群优化算法--模拟维度PSO（SDPSO），它结合了模拟退火来更新全局最优解，以及维度学习策略来减少粒子退化，避免局部最优解，并增强算法的搜索能力。SDPSO算法的表现优于其他算法，包括GA、差分进化、GWO、ACO和SA，它在更短的时间内为无人机提供了一条满足其约束条件的最佳路径。可以有效地解决复杂三维环境中无人机的路径规划问题，提高其整体效率和自主性。

关键技术

在本文中，提出了一种新的路径规划算法SDPSO算法框架，它的优化策略包括模拟退火算法和维度学习策略。模拟退火算法用于改进全局最优解的更新策略，利用随机梯度下降方法逼近全局最优解。维度学习策略被应用于减少粒子群的振荡，提高收敛速度。基于维度学习策略，每个粒子会选择合适的维度来集中对最优解的搜索，避免在搜索过程中偏离更优的位置。这两种优化方法提高了粒子下降速度，避免局部最优解，增强搜索能力，适用于处理UAVs在复杂三维环境中的路径规划问题。

该方法的创新和贡献如下：

1.提出了一种新的SDPSO算法来解决无人机3-D路径规划问题；

2.在SDPSO算法中，每个粒子都集成了全局最优解的有用信息，减少了粒子在进化过程中的退化现象，提高了收敛速度。全局最优解的迭代更新过程与SA算法相结合，增加了粒子的搜索能力，提高了SDPSO算法的性能。

算法介绍

1. 路径规划模型

1. 地形和威胁建模

图1

无人机的路径规划是在解空间中寻找最优或次优解，图1是一组避免山脉和各种威胁的无人机飞行路径。解空间可以表示为

山峰、雷达或其他危险区域被认为是无人机无法通行的区域。将这些严重影响无人机飞行安全的区域称为障碍区域。障碍物信息对于无人机的路径规划至关重要，它直接决定了路径规划的质量，可以通过通信设备和机载传感器进行实时预加载或更新。

障碍物的数学模型定义为：

道路穿越危险区域的成本函数f_1显示如下：

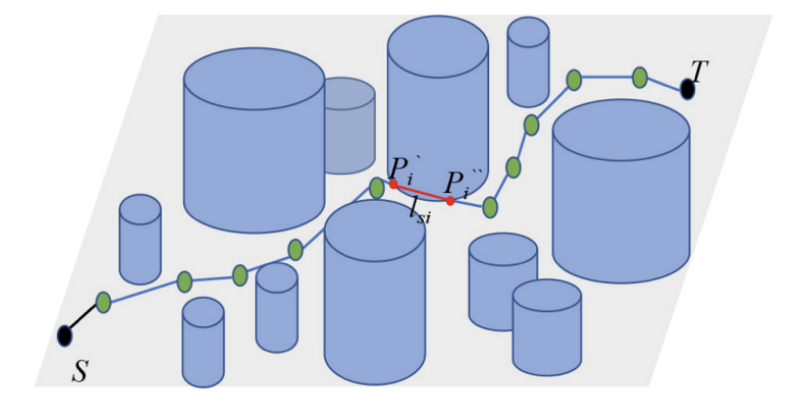
如图2所示，其中l_si为危险区域路径的长度，dash_punk为通过危险区域路径的长度惩罚系数。

图2

与路径长度相关联的成本函数f_2如下所示：

2. 无人机飞行特性的约束建模

图3

如图3所示，一个有效的路径不仅要避免山脉和各种威胁，而且要满足无人机的物理约束，如偏航角α_i和俯仰角β_i。

综合偏航角α_i和俯仰角β_i，成本函数f_3显示如下：

当无人机的路径高度接近地面高度时，无人机撞击地面的风险增加。当路径高度过高时，无人机在特殊任务中很容易被敌方雷达探测到，并且无法达到最小化飞行路径的原始目的。无人机的路径预计将在一个合适的高度。与路径高度相关的成本函数f_4如下所示：

3. 适应度函数建模

路径的质量经常通过适应度函数来评估。考虑到路径长度、路径高度、无人机飞行特性以及与路径质量相关的安全约束，可以定义一个评估路径质量的适应度函数为

2. SDPSO算法

1）粒子初始化

图4  粒子结构

在利用SDPSO算法求解无人机的路径规划问题时，求解空间由每个可行路径组成，粒子维数D为确定每条路径的中间节点数。给定粒子维数D和当前迭代次数t，第i个粒子的位置为x_t-i和速度v_t-i。个体的历史最优位置和全局最优解可以分别表示为p_t-i和g_t-i。

2）全局最优解的更新策略：作为一个贪婪的算法，SA算法的核心思想是比较概率p，接受p较大的方案，以避免陷入一个局部最优解。伪代码如下所示：

参数p表示次优解被接受的概率。当p过大时，算法的收敛性较差；当p过小时，算法效率不高，容易陷入局部最优解。

其中，T为当前系统的温度。如果T太大，则会导致概率p趋于1，这意味着该算法将接受具有更高概率的次优解。在算法迭代的后期阶段，如果概率p太大，则该算法将难以收敛。用T_t+1 = r×T_t，r更新T是控制[0,1]中温度变化速率的参数。

其中，K为最大迭代次数，t为当前迭代次数。如果r太大，使用该算法找到全局最优解的概率就会更大。但这将是一个非常耗时的过程。相反，如果r太小，搜索过程将会更快，但它可能会陷入局部收敛。因此，r采用随种群迭代线性递减的方法进行更新。

3）SDPSO的加速收敛：在SDPSO中引入了SA算法来更新全局最优解gt，从而使总体中每个粒子的振荡可能更加严重。这种现象降低了它的收敛速度。为了克服这一缺点，本文采用了DLS方法。如算法3所示，记录每个粒子的连续非更新数计数，当计数超过某个阈值m时，将根据全局最优解gt更新当前粒子在每个维中的位置x_t_i。伪代码如下所示：

其中，m如下式所示：

其中，M_max和M_min分别表示上界和下界。当m太大时，算法收敛速度太快，但种群多样性下降。搜索空间多样性的减少导致局部最优解。如果m太小，则该算法可能无法有效地工作。

3. 无人机路径规划的SDPSO算法：SDPSO算法将全局最优解gt的更新与SA算法相结合，增强了解空间的多样性，使其跳过局部最优解，提高了搜索全局最优解的能力。此外，还嵌入了DLS来克服粒子在演化过程中的振荡。根据DLS，每个粒子按维数集成了全局最优解维数的有益信息，减少了粒子在演化过程中的退化，提高了算法的收敛速度。伪代码如下所示：

实验结果分析

1. 仿真参数设置

表1展示了算法参数设置；

表2展示了模型参数设置；

图5展示了简单山地模型；

图6展示了复杂山地模型。

表1

表2

图5

图6

2. 简单环境中算法对比结果

图7 不同算法的无人机路径规划

图7中有6条路径，对应于六种不同的相同环境约束下的无人机路径规划算法。虽然六种路径远离地形障碍，但很明显，六种算法的路径规划结果是不同的。由PSO算法得到的路径是最差的。该路径有轻微的振荡，导致路径不稳定，并增加了这个路径的长度。这不利于无人机任务的实施。由SDPSO算法得到的路径最平滑，质量最好。

图8  适应度值随着迭代的变化

图8显示了6个算法的收敛曲线。与其他算法相比，SDPSO算法得到的适应度函数的值明显最小，其次是TSLPSO、DGBCO、GWO和RPSO。由PSO算法得到的适应度函数的值最高。换句话说，SDPSO算法得到的路径更好，而PSO、RPSO、GWO、DGBCO和TSLPSO规划的轨迹被困在局部最优解中。另一方面，SDPSO算法的收敛速度最快，当迭代次数约为120时，可以得到最优解，远远优于其他算法。

表3 重复100次后的适应度值比较

在相同的条件下，实验重复了100次。从表3可以看出，SDPSO算法得到的适应度函数的值最小，其次是TSLPSO、DGBCO、RPSO和GWO。由PSO算法得到的适应度函数的值最高。与PSO、DGBCO、GWO、TSLPSO和RPSO相比，SDPSO算法的最优、最差和平均值最小。以上结果表明，SDPSO具有更好的全局优化能力。

3. 复杂环境中算法对比结果

图9 不同算法的无人机路径规划

图10 适应度值随着迭代的变化

表4 重复100次后的适应度值比较

复杂环境中不同算法的对比结果如上图表所示。SDPSO在最佳值、最差、平均数和性病方面都有最好的性能。此外，SDPSO的均值最低，说明SDPSO算法的收敛速度最快。显然，当飞行环境更加复杂时，收敛速度和SDPSO算法的全局优化能力仍然很好。

基于以上实验结果，当使用SA算法更新全局最优解时，它可以帮助SDPSO算法增加搜索空间的多样性，使其跳过局部最优解。每个粒子集成了全局最优解的有用信息，减少了粒子在演化过程中的退化，提高了算法的收敛速度。与其他算法相比，SDPSO算法具有更好的全局优化能力和更快的搜索速度。

总结