工程实现

启发式识别展平函数

事实证明，二进制文件中的一些非库函数未展平。我设计了一种启发式方法来确定给定函数是否被展平。展平的函数将一个变量(块号变量)与jz和jg指令中的数字常量进行比较，这些数字常量似乎是伪随机生成的。有了这种特征就可以编写用于启发式确定某个函数是否被展平的算法。
1.遍历函数中的所有microcode(SDK提供了mbl_array_t::for_all_topinsns函数)。

2.对于每一个将变量和常数比较的jz/jg指令，记录相应的信息(变量，变量和常量比较的次数，对应的所有常量)。

3.选择被比较次数最多的变量对应的所有常量。

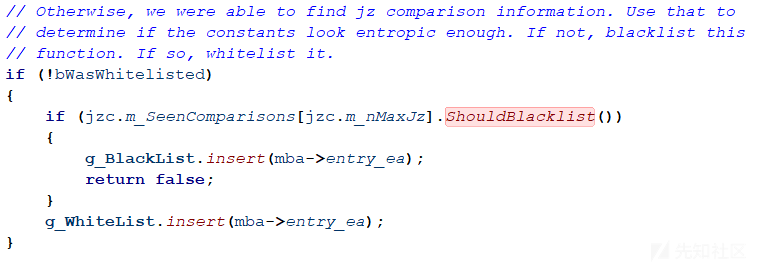
4.计算常量中为1的位数然后除以总位数，因为这些常量应该是伪随机生成的，所以这个值应该接近0.5。如果这个值在0.4和0.6之间则可以确定该函数已被展平。

简化图结构

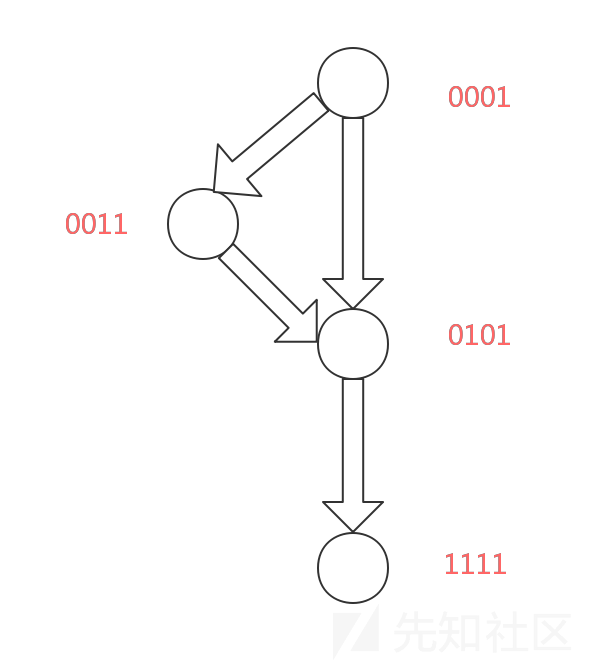
展平的函数有时具有直接导致其它跳转的跳转，或者有时microcode翻译器插入以其它goto指令为目标的goto指令。例如在下图中，块4包含goto到块8的指令，而块8又包含goto到块15的指令。

如果@X块以goto @N指令结尾，并且@N块为一条goto @M指令，则将goto @N更新为goto @M。对于任意数量的goto以递归的方式应用此过程。
在RemoveSingleGotos函数中第一次遍历所有的块，如果该块的第一条指令是goto指令则记录下目的地址到forwarderInfo中，否则forwarderInfo为-1。

第二次遍历所有的块，如果该块的最后一条指令是call或者该块有不止一个后继者则跳过，考虑两种情况：最后一条指令是goto和最后一条指令不是goto。如果最后一条指令是goto指令，将iGotoTarget设置为goto的目标；如果最后一条指令不是goto指令，将iGotoTarget设置为其唯一后继者。

在while循环中将下一个块设置为forwarderInfo[iGotoTarget]，如果该块已经在while循环中遇到过说明这是一个死循环，将bShouldReplace设置为false并退出。如果forwarderInfo为-1说明遇到了一个第一条指令不是goto指令的块，也退出。只要遇到了一个第一条指令是goto指令的块就将bShouldReplace设置为true。

如果最后一条指令是goto指令，将目的地址更改为while循环中的最后一个块；如果最后一条指令不是goto指令，增加一个目的地址为while循环中的最后一个块的goto指令。修改相应的前驱者和后继者信息。

提取块号信息

许多平坦化函数使用两个变量来实现与块号相关的功能。对于使用两个变量的情况，该函数的基本块更新的变量与switch(block)所比较的变量不同。这里将这两个变量分别称为块更新变量和块比较变量。在switch(block)开始时，将块更新变量的值复制到块比较变量中，此后所有后续比较均参考块比较变量。下图中switch(block)从@2块开始，@1块为ST18_4.4变量分配了一个数值。switch(block)中第一个比较在第2.3行，跟此变量相关。第2.1行将该变量复制到另一个名为ST14_4.4的变量中，然后将其用于后续比较(如第3.1行以及此后的所有switch(block)比较)。

然后，函数的平坦化块更新变量ST18_4.4。

(令人困惑的是，函数的平坦块更新了两个变量，但是仅使用了对块更新变量ST18_4.4的赋值。块比较变量ST14_4.4在使用其值之前，在第2.1行中被重新定义了)。
因此，我们实际上有三个任务：
1.确定哪个变量是块比较变量(我们已经通过熵检查得知)。
2.确定是否存在块更新变量，如果存在，则确定它是哪个变量。
3.从jz针对块比较变量/块更新变量的比较中提取数字常数，以确定平坦块编号到mblock_t的映射。
首先，我们获取switch(block)之前的第一个块。从函数的开头开始一直向后移动，直到下一个块有多个前驱者。此时这个块就是switch(block)之前的第一个块(例如上面例子中的@1块)，下一个块就是switch(block)(例如上面例子中的@2块)。

找到switch(block)之前的第一个块中所有对变量赋常量值的指令，如果找到了块比较变量说明此时不存在块更新变量。

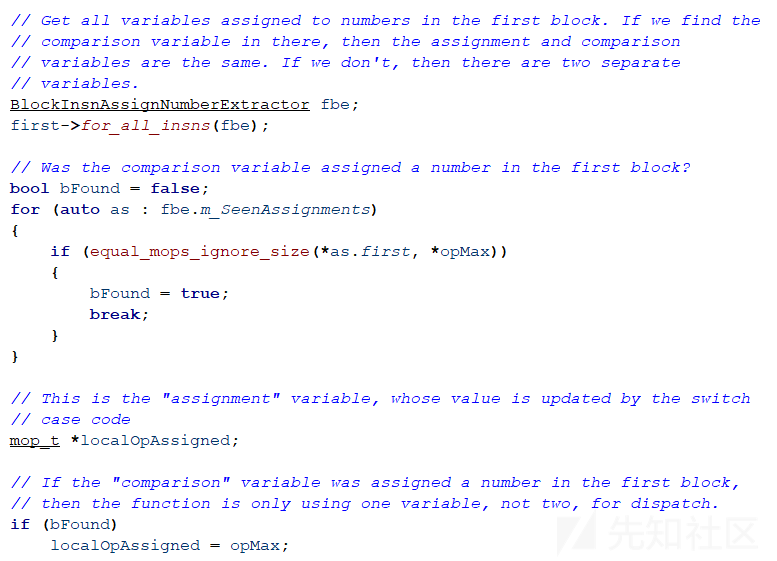
否则说明此时存在块更新变量，如果switch(block)之前的第一个块中对某变量赋常量值并且在switch(block)中将该变量拷贝给块比较变量，那么这个变量就是块更新变量。


从jz针对块比较变量(位于switch(block)的块更新变量)的比较中提取数字常数，以确定平坦块编号到mblock_t的映射。

取消控制流平坦化

我们现在知道哪个变量是块更新变量/块比较变量。我们还知道哪个平坦块编号对应于哪个mblock_t。对于每个展平的块，我们需要确定块更新变量的值。
如前所述，平坦块有两种情况：
展平的块始终将块更新变量设置为单个值(对应于无条件分支)。
展平的块使用x86 CMOV指令将块更新变量设置为两个可能值之一(对应于条件分支)。
对于如下所示的第一种情况找到一个数字就可以了。下图中块更新变量为ST14_4.4，我们的任务是在第9.4行找到数字分配。现在可以将最后一行的goto更改为对应的mblock_t。


对于如下所示的第二种情况需要确定ST14_4.4可能被更新为0xCBAD6A23(6.0)或0x25F52EB5(7.0)。

更新jz为true执行的块的goto指令(上面的例子中，将@8块的goto指令更新为goto @6)。

将jz为true执行的块拷贝到jz为false执行的块(上面的例子中，将@8块拷贝到@7块)。

更新jz为false执行的块的goto指令(上面的例子中，将@7块的goto指令更新为goto @9)。

其它问题

平坦块可能包含许多mblock_t

如上述第一种情况，mblock_t可以通过一个以上的mblock_t来实现平坦化的块，或者如上述第二种情况，mblock_t可以通过三个以上的mblock_t来实现平坦化的块HexRays在函数调用边界上分割基本块，因此单个平坦块可以有任意数量的mblock_t。由于查找分配给块更新变量的数值需要从平坦区域的末端开始工作，所以需要知道该区域的末端在哪里。这里通过计算函数的支配树(dominator tree)并找到将回到switch(block)并且由平坦块块头支配的块解决了这个问题。计算支配树的算法如下所示。如果一个函数含有X个基本块则每个基本块用X位的bitset来表示支配关系，第Y位为1表示基本块Y支配基本块X。初始化时每个基本块都支配每个基本块，即每个基本块的bitset每一位都为1，然后将第一个基本块的bitset设置为只有第一位为1，即对于第一个基本块只有它自己支配自己。然后遍历基本块，更新该基本块的bitset为它的bitset和它的前驱的bitset的与，然后设置该基本块自己支配自己。一直重复这样循环，直到bitset不再发生改变。

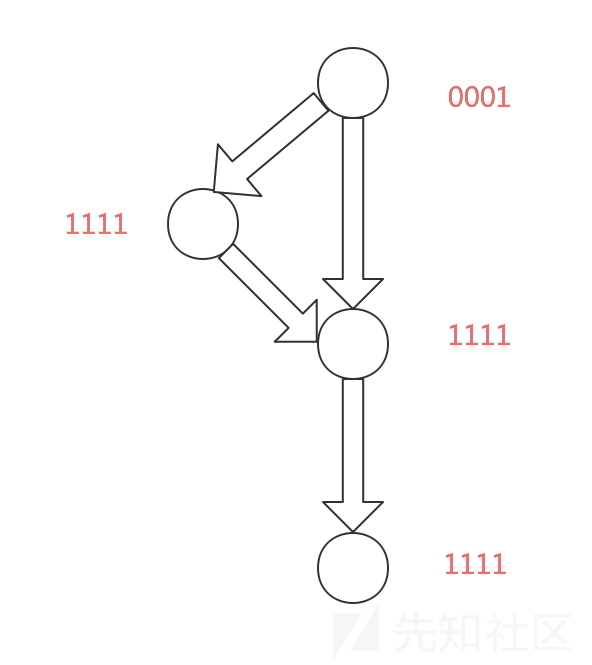
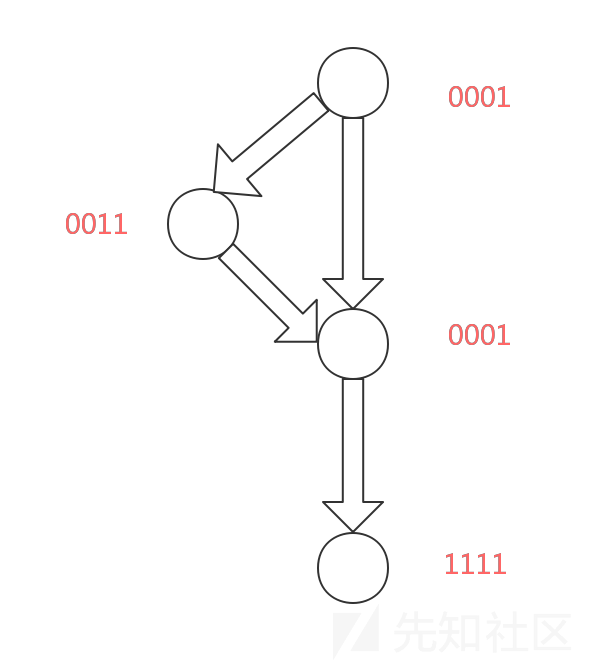
查找分配给块更新变量的数值

查找分配给块更新变量的数值有些情况下很简单，有些情况下很困难。有时HexRays的常量传播算法会创建将常量直接移动到块更新变量中的microcode或者通过几个寄存器或栈变量对块更新变量赋值。FindNumericDefBackwards函数从一个块的底部开始搜索对块更新变量的赋值。如果块更新变量是由另一个变量赋值的，它将执行递归搜索。一旦最终找到数字常量赋值则返回true。如果找到了支配该块的mbClusterHead块仍然没有找到则返回false。 然而当平坦化块通过指针写入内存时上述算法将不起作用。如下所示，在平坦化块的开头常量被写入寄存器，然后被保存到栈变量中。

稍后用指针写入内存。

最后从栈变量中读取。

这给我们带来的问题是HexRays需要证明中间的内存写入不会覆盖已保存的数据。通常，指针混叠是一个无法确定的问题，这意味着不可能编写算法来解决它的每个实例。当FindNumericDefBackwards函数返回false并且最后是从栈变量中读取时调用FindForwardStackVarDef函数转到平坦化块的开头查找。以上面的情况为例，跳到第一个代码片段并且找到分配给var_B4和var_BC的常量。这样做不安全，但是恰好适用于此样本中的每个函数，并且很可能适用于该混淆编译器编译的每个样本。

总结

控制流平坦化这一混淆技术早已经在代码保护工具和恶意代码样本中屡见不鲜，Rolf Rolles的方法为解决这一问题提供了新的思路。目前idapython已经提供了Rolf Rolles所开源代码的python版本pyhexraysdeob。国外有研究人员基于Rolf Rolles的成果对APT10样本中类似的混淆进行了处理，也取得了比较好的效果：Defeating APT10 Compiler-level Obfuscations。