作者:bear该篇文章是我学习过程的一些归纳总结,希望对大家有所帮助。最近因为 AI 大火,搞的我也对 AI 突然也很感兴趣,于是开启了 AI 的学习之旅。其实我也没学过机器学习,对 AI 基本上一窍 2023-4-28 18:1:41 Author: 腾讯技术工程(查看原文) 阅读量:29 收藏
作者:bear
该篇文章是我学习过程的一些归纳总结,希望对大家有所帮助。
最近因为 AI 大火,搞的我也对 AI 突然也很感兴趣,于是开启了 AI 的学习之旅。其实我也没学过机器学习,对 AI 基本上一窍不通,但是好在身处在这个信息爆炸的时代,去网上随便一搜发现大把的学习资料。
像这个链接里面:https://github.com/ty4z2008/Qix/blob/master/dl.md 就有很多资料,但是这相当于大海捞针。在学习之前我们先明确自己的目的是什么,如题这篇文章是入门强化学习,那么就需要定义什么是入门。在很多强化学习里面,学习深度强化学习的第一个算法都是 DQN,这个算法也足够好学和实用,所以本篇文章就以搞懂它做为目标,表示入门。下面是我的学习计划:
如果和我一样一点基础也没有,并且概率论和线性代数的知识差不多都忘完了,那么可以去看一下相关课程学习一下,如果不关注公式啥的,这一步可以先忽略,大约周末一天时间就可以搞定; 然后如果对机器学习也一点基础都没有的话,可以先看吴恩达的课程,有个大致的理解,然后去看李宏毅的课程作为补充,如果单纯的想入门学习强化学习,那么只需要看前几节讲完神经网络那里就差不多了,这个视频课程估计要看 25 小时左右; 学完之后可以跟着《动手学深度学习 https://hrl.boyuai.com/ 》一起动手学习一下我们上面学到的概念,写写代码,如果只是入门的话看前五章就好了,本篇文章的很多资料也是整理自这本书,大约 10 小时左右; 接下来可以看看 B 站王树森的深度学习的课程,可以先看前几节学习一下强化学习的基础知识点,大约 5 小时左右; 到这个阶段估计还是懵的,需要去上手做点项目,那么可以看《动手学强化学习》这本书,已经开源了 https://hrl.boyuai.com/ ,只看到 DQN 的部分,大约十几小时。
概念
对于新学习一个基础的内容,我们先从概念入手。
强化学习能做什么
强化学习(Reinforcement Learning,RL)是机器学习领域的一个重要分支,它关注智能体如何通过与环境的交互来学习和优化策略,以实现长期回报的最大化。强化学习已经在许多领域取得了显著的成功,以下是一些主要的应用场景:
游戏:强化学习在游戏领域取得了很多突破性的成果,如 DeepMind 的 AlphaGo 在围棋比赛中战胜世界冠军,以及 OpenAI 的 Dota 2 AI 在电子竞技比赛中战胜职业选手。这些成功表明,强化学习能够帮助智能体学习复杂的策略和行为,甚至超越人类的表现。 机器人学:强化学习在机器人学领域有广泛的应用,如机器人控制、导航和自主学习。通过强化学习,机器人可以学会在复杂的环境中自主执行任务,如搬运物品、避障导航、飞行控制等。 自动驾驶:强化学习可以用于自动驾驶汽车的控制和决策。通过与环境的交互,自动驾驶汽车可以学会在复杂的道路环境中保持安全驾驶,规避障碍物,遵守交通规则等。 推荐系统:强化学习可以用于个性化推荐系统,通过学习用户的行为和喜好,智能地推荐合适的内容。例如,网站可以使用强化学习算法来优化新闻、广告或产品推荐,从而提高用户的满意度和留存率。 自然语言处理:强化学习在自然语言处理领域也有广泛的应用,如对话系统、机器翻译、文本摘要等。通过强化学习,模型可以学会生成更符合人类语言习惯的文本,提高语言理解和生成的质量。 资源管理:强化学习可以用于优化资源管理问题,如数据中心的能源管理、通信网络的流量调度等。通过学习和优化策略,强化学习可以实现资源的高效利用,降低成本,提高性能。 金融:强化学习在金融领域也有一定的应用,如股票交易、投资组合优化等。通过强化学习,智能体可以学会根据市场变化调整投资策略,从而实现收益的最大化。
以上是 chatgpt 告诉我的强化学习应用,其实就个人来说,强化学习最多的应用领域还是打游戏,B 站上面有很多利用强化学习实现各种风骚操作打游戏的训练视频还是蛮有意思的,比如:
https://www.bilibili.com/video/BV1Dg4y137Cq 强化学习玩只狼;
https://www.bilibili.com/video/BV1nD4y1j7QL 强化学习玩空洞骑士;
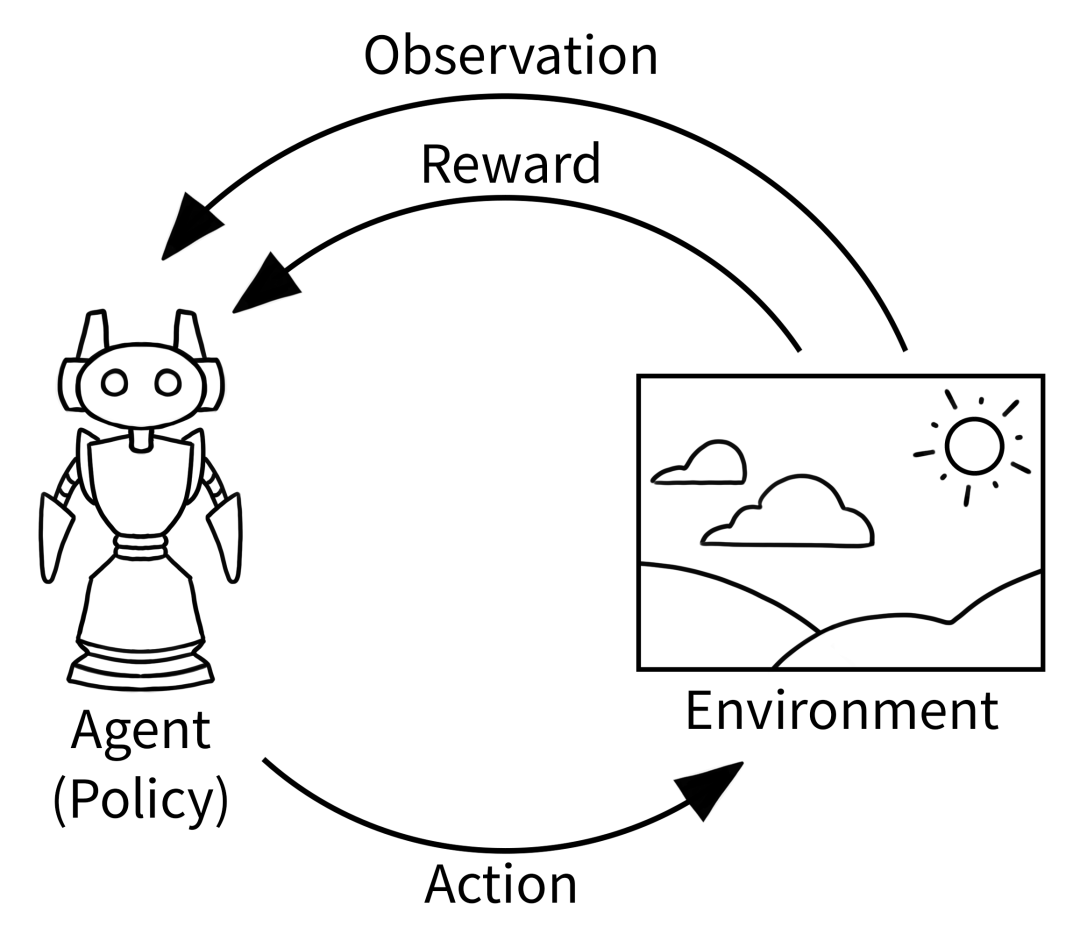
反正看到上面这些我是觉得酷毙了(绝对不是因为我玩的菜)。所以简单的说,强化学习(Reinforcement learning,RL)是一类机器学习算法,用于描述和解决有智能体(agent)和环境(environment)交互的问题。在强化学习中,智能体通过与环境不断交互、观察环境和执行动作来学习最优策略,以达到最大化某种累积奖励的目标。
强化学习三个要素
具体来说,强化学习通常涉及以下三个要素:
状态(State):描述智能体所处的环境状态。 动作(Action):智能体可以采取的动作。 奖励(Reward):智能体根据执行动作和观察结果获得的奖励。
强化学习的核心思想是基于试错学习,即智能体通过尝试不同的动作并观察结果来逐步调整自己的行为策略,以取得更高的奖励。通常,强化学习算法会利用回报(reward)或价值函数(value)来评估一种行为策略的好坏,并在学习过程中不断更新和调整该策略,以达到最大化累积奖励的目标。
构造只有动作和奖励的环境
对于我们来说,一开始直接从三个要素开始进行可能会比较困难,那么我们可以从一个简单的环境入手,这个环境只有动作和奖励,是多臂老虎机(multi-armed bandit,MAB)问题。
大家应该或多或少都接触过老虎机,我们这里假设这些老虎机是一个纯粹的老虎机,每次出奖的概率和拉动拉杆的次数没有关系,并且有 K 台老虎机,每台老虎机的奖励概率都不一样,每次拉动其中一根拉杆,就可以从该拉杆对应的奖励概率分布中获得一个奖励 r。
每次选择一个老虎机,然后去拉动它对应就是一个动作 a,那么对应的在拉动了无数个这样的机器之后就可以得到这些老虎机的奖励期望,记为 ,那么在这些拉杆中,至少存在一根拉杆,它的期望奖励不小于拉动其他任意一根拉杆,我们将该最优期望奖励表示为 。
由于我们拉动的拉杆不是每次都是最优的那个,所以存在拉动当前拉杆的动作与最优拉杆的期望奖励差,即 ,也称为悔恨度(regret)。我们把操作 T 次之后的期望奖励差加总和就是 ,多臂老虎机问题的目标为最大化累积奖励,等价于最小化 。
为了实现最大化累积奖励,那么我们就需要计算出老虎机的奖励期望,那么如何在不知道中奖概率的情况下计算出老虎机的期望呢?我们有两种方式
一种是收集足够的游戏数据,每种奖励的中奖次数除以总游戏次数,即可得到该奖励的估算概率,然后乘以奖励金额计算每个奖励的期望即可; 另一种是累计更新期望进行增量式的期望更新,这也是我们强化学习里面将采用的; 初始化计数器 N(a) = 0 和奖励期望估计值 ;
fot t = 1 -> T do 1.选取某根拉杆,该动作记为
2.获得奖励
3.更新计数器:
4.更新期望奖励估计:
End for
上面之所以可以如此进行增量式期望更新其实是有下方公式(1)可以推导的:
期望更新的问题解决了,那么我们该处理行动的问题,也就是在这 k 个老虎机中我们应该选择哪个?我们下面看看 ε 贪心方法。
ε 贪心方法(ε -Greedy method)
对于一个 10 臂老虎机,我们要把所有的拉杆都拉动一下才知道哪根拉杆可能获得最大的奖励,通常如果我仅靠已知的信息仅仅来自有限次的交互观测,所以当前的最优拉杆不一定是全局最优的,这也很好理解。我已我们需要增加探索(exploration)这种方式进行行动,也就是让我们的选择的行动有一定概率去尝试一些没尝试过的选择,这样兴许会发现期望值更高的选择。
所以在 ε 贪心方法中去尝试没有选择过的行动就叫做探索(exploration),在现有的数据中找到期望最大的值作为行动叫做利用(Exploit)。ε 贪心方法就是设定一个 ε 值, 用来指导我到底是探索(Explore)还是利用(Exploit)现有的数据。
比如将 ε 设定为 0.1,以保证将 10%的次数投入在探索(Explore),90%的次数用于利用(Exploit),因为一直在探索,而不仅仅局限于当前的交互观测,所以当尝试的次数足够多时当前的最优拉杆是可以趋近于最优的拉杆,公式如下:
但是如果 ε 的值一直不变也是会有问题的,其实也很容易想到,假设 ε 设定为 0.1,那么再怎么最优也有 10%的概率是随机的,那么我们在上面提到了 被称为悔恨度(regret), 一定会随着实验的次数不停增长:
由于我们随着实验次数的增加其实对期望的估计会越来越准确,那么对于有限的 K 臂老虎机这种情况,实际上可以尝试选择 ε 值随时间衰减的贪婪算法,比如可以设置为反比例衰减,公式为:ε = 1/t。这样我们可以看到这个算法明显优于原来的随机取值:
最后我们根据上面的方法逐步训练算出了各个老虎机的期望,用期望形成了一张表,然后我们就可以根据这种选择最大期望的老虎机进行行动了。
上面所讲的这些方法都是没有状态的,下面我们加入状态看看该如何进行训练。
满足三要素有限步骤环境
到这里我们把状态也添加进来,也就是说每次行动之后,自身所处的状态会变,那么智体又该如何做决策。需要注意的是,我们为了简化,这里仍然有一条件,那就是行动和状态是有限的,不会很多。
马尔可夫决策过程(Markov decision process,MDP)
在继续往下之前先来看看什么是 MDP。上面讲的多臂老虎机实际上是没有包含状态(State)的,而马尔可夫决策过程包含状态信息以及状态之间的转移机制。
我们用 St 表示所有可能的状态组成状态集合,如在某时刻 t 的状态 St 通常取决于时刻 t 之前的状态。我们将已知历史信息(S1,...St)时下一个时刻状态为 St+1 的概率表示成 。当且仅当某时刻的状态只取决于上一时刻的状态时,一个随机过程被称为具有马尔可夫性质(Markov property),用公式表示为:
即下一个状态只取决于当前状态,而不会受到过去状态的影响。
我们通常用元组 (S,P)描述一个马尔可夫过程,其中 S 是有限数量的状态集合,P 是状态转移矩阵(state transition matrix)。状态转移矩阵定义了所有状态对之间的转移概率,即:
矩阵 P 中第 i 行第 j 列元素:
表示从状态 转移到状态 的概率,我们称 为状态转移函数。从某个状态出发,到达其他状态的概率和必须为 1,即状态转移矩阵 P 的每一行的和为 1。
在马尔可夫过程的基础上加入奖励函数 r 和折扣因子 γ,就可以得到马尔可夫奖励过程(Markov reward process),一个马尔可夫奖励过程由(S,P,r,γ)构成。在一个马尔可夫奖励过程中,从第 t 时刻状态 St 开始,直到终止状态时,所有奖励的衰减之和称为回报Gt(Return),公式如下:
这上面的公式其实也很符合常识,对于未来的预期通常预测是不准确的,那么我们的的回报折扣力度力度会更大一些,所以每往后推一个时刻会多乘一个折扣因子。
在马尔可夫奖励过程中,一个状态的期望回报(即从这个状态出发的未来累积奖励的期望)被称为这个状态的价值(value)。所有状态的价值就组成了价值函数(value function),价值函数的输入为某个状态,输出为这个状态的价值。我们将价值函数写成 ,展开为:
态,输出为这个状态的价值。我们将价值函数写成 ,展开为公式(2):
一方面,即时奖励的期望正是奖励函数的输出
一方面,即时奖励的期望正是奖励函数的输出,;另一方面,等式中剩余部分 可以根据从状态s出发的转移概率得到,即可以得到:
上式就是马尔可夫奖励过程中非常有名的贝尔曼方程(Bellman equation)。我们将所有状态的价值表示成一个列向量,于是我们可以将贝尔曼方程写成矩阵的形式:
马尔可夫决策过程(Markov decision process,MDP)在上面的马尔可夫奖励过程(MRP)的基础上加上了动作 A,那么马尔可夫决策过程(MDP)由元组(S,A,P,r,γ)构成,其中:
S 是状态的集合;
A 是动作的集合;
γ 是折扣因子;
r(s,a)是奖励函数,此时奖励可以同时取决于状态和动作,在奖励函数只取决于状态 s 时,则退化为r(s);是状态转移函数,表示在状态执行动作 之后到达状态的概率。
MDP 根据奖励函数和状态转移函数得到 St+1 和 Rt 并反馈给智能体。智能体的目标是最大化得到的累计奖励,所以会根据当前状态从动作的集合 A 中选择一个动作的函数,被称为策略,这个策略需要智体在行动过程中训练出来。
上面的策略描述可能比较抽象,可以举个例子,比方我们在玩下面这个悬崖漫步(Cliff Walking)游戏的时候,我们的目的是从左下角走到右下脚,当前状态是下面这个位置,那么我的行动可以有三种:向左、向右、向下,那么该选择哪种行动以达到我们的游戏收益的最大化就是策略。
智能体的策略(Policy)通常用字母 表示,策略 是一个函数,表示在输入状态 s 情况下采取动作 a 的概率。在 MDP 中,由于马尔可夫性质的存在,策略只需要与当前状态有关,不需要考虑历史状态。
我们用 表示在 MDP 中基于策略 的状态价值函数(state-value function),定义为从状态 s 出发遵循策略 能获得的期望回报,数学表达为:
在 MDP 中,由于动作的存在,我们额外定义一个动作价值函数(action-value function)。我们用 表示在 MDP 遵循策略 π 时,对当前状态 s 执行动作 a 得到的期望回报:
那么在使用策略 π 中,状态 s 的价值等于在该状态下基于策略 π 采取所有动作的概率与相应的价值相乘再求和的结果:
使用策略 π 时,状态 s 下采取动作 a 的价值等于即时奖励加上经过衰减后的所有可能的下一个状态的状态转移概率与相应的价值的乘积:
我们通过简单推导就可以分别得到两个价值函数的贝尔曼期望方程(Bellman Expectation Equation)公式(3):
上面这两个函数需要记住了,之后的一些强化学习算法都是据此推导出来的。
强化学习的目标通常是找到一个策略,使得智能体从初始状态出发能获得最多的期望回报。那么我们就需要找到最优的状态价值函数,以及最优的动作价值函数,可以记为:
为了使 最大,我们需要在当前的状态动作对(s,a)之后都执行最优策略。于是我们得到了最优状态价值函数和最优动作价值函数之间的关系:
最优状态价值是选择此时使最优动作价值最大的那一个动作时的状态价值:
那其实我们也可以得出贝尔曼最优方程公式(4):
上面这个方程看起来很好,但是实际上我们需要知道所有的状态转移函数和奖励函数,这在很多场景下是无法实现的,所以我们需要使用蒙特卡洛方法做一个近似估计。
蒙特卡洛方法
蒙特卡洛方法它是一种通过随机抽样来解决统计问题的方法。其基本思想是通过在特定区域内进行随机抽样,然后根据抽样结果来估计某个量的值。
比如下面我们需要计算一个半径为 1 的圆形的面积。我们知道圆的面积公式是 A = πr²,其中 r 是半径。在这个例子中,半径 r = 1,我们实际上想要估计圆周率 π 的值,那么可以在下面的正方形中随机地抽取大量的点,统计落在圆内点的数量,然后除以总抽样点的数量。这个比值就是圆形面积与正方形面积之比。随着抽样点数量的增加,我们的估计值将越来越接近圆的真实面积,即 π * r²,然后我们就可以根据面积和半径算出圆周率 π 的值。
所以我们可以延申一下,状态的价值期望等于
在蒙特卡洛方法中,我们从状态 s 开始模拟 N 个轨迹,每个轨迹的累积折扣回报分别为 G_1, G_2, ..., G_N。状态 s 的价值估计 V(s) 可以表示为:
计算回报的期望时,除了可以把所有的回报加起来除以次数,还有一种增量更新的方法。对于每个状态 S 和对应回报 G,进行如下计算公式(5):
这种增量更新的方式我们在上面已经讲过,只是将它推导到价值函数中。根据上面的公式,我们将 替换成 α,表示对价值估计更新的步长,可以将它取为一个常数,这样可以在当前步结束即可进行计算。又有下面公式(6):
所以可以用当前获得的奖励加上下一个状态的价值估计来作为在当前状态会获得的回报,即:
其中 通常被称为时序差分(temporal difference,TD)误差(error),时序差分算法将其与步长的乘积作为状态价值的更新量,这样我们只需要知道下一个状态的价值和当前状态的价值是多少就可以更新最新的价值了。下面我会用这个公式带入到我们的强化学习的算法中。
Q-learning 算法
到这里来到了我们第一个强化学习算法,它是我们下面将要讲到的 DQN 的弱化版本。Q-Learning是强化学习算法中value-based的算法,value 指的就是我们上面提到的动作价值 Q(s,a),就是在某一个时刻的状态 s 下,采取动作 a 能够获得收益的期望。
为了能够得到这个收益的期望,Q-learning 使用了一张表,里面记录了所有的状态和动作所能带来的 Q 值,我们把这张表叫做 Q 表。比如对于我们的悬崖漫步来说共有 48 个格子加上上下左右 4 个动作:
那么我们可以用它来初始化我们的表格,纵坐标表示格子序号,横坐标表示动作:
比如当前智能体(agent)在 s1 这个状态上,下一步该做什么行动就会去这个表里面找哪个 Q 值最大,发现向下行动是最大的,那么就会往下走,这个时候我们获取到 Q(s1,下) 乘上一个衰减值 gamma (比如是 0.9) 并加上到达下一个状态时所获取的奖励 R ,把这个值作为现实中 Q(s1,下)的值,也就是 ‘Q 现实’,之前的根据 Q 表 得到的 Q(s1,下)是 Q 表估计的值,也就是‘Q 估计’, 有了 Q 现实 和 Q 估计,就可以更新 Q(s1,下)的值,公式如下:
上面公式中 就是Q 现实,α 是学习率, 来决定这次的误差有多少是要被学习的, alpha 是一个小于 1 的数,γ 是对未来 reward 的衰减值,我们在上面介绍过。
那么有了这个公式在加上我们每一步中得到的四元组 就可以不停的更新我们的 Q 表,数据中的 S 和 A 是给定的条件,R 和 S'皆由环境采样得到。Q-learning 算法的具体流程如下:
初始化 Q(s,a) for 序列 e = 1 -> E do: 用 ε -Greedy 策略根据 Q 选择当前状态 s 下的动作 a 得到环境反馈的 r,s‘ 得到初始状态 s for 时间步 t = 1-> T do: End for End for
下面代码是 chatgpt4 生成的,我小改了一下:
import numpy as npimport gymnasium as gym
env = gym.make('CliffWalking-v0',render_mode="human")
ACTIONS = env.action_space.n
# 定义环境参数
ROWS = 4
COLS = 12
# 定义 Q-learning 参数
EPISODES = 500
ALPHA = 0.1
GAMMA = 0.99
EPSILON = 0.1
# 初始化 Q-table
q_table = np.zeros([ROWS*COLS, ACTIONS])
# 定义一个函数根据 Q-table 和 ε-greedy 策略选择动作
def choose_action(state, q_table, epsilon):
if np.random.random() < epsilon:
# 随机选择一个动作
return np.random.randint(ACTIONS)
else:
# 选择具有最大 Q 值的动作
return np.argmax(q_table[state])
# 定义一个函数实现 Q-learning 算法
def q_learning():
# 进行多次训练以更新 Q-table
for episode in range(EPISODES):
# 从起始状态开始
state, _ = env.reset()
done = False
count = 0
# 在每个训练回合中不断采取动作,直到达到终点
while not done and count < 200:
count += 1
# 选择一个动作
action_index = choose_action(state, q_table, EPSILON)
# 获取下一个状态、奖励和是否到达终点
next_state, reward, done, _, _ = env.step(action_index)
# 更新 Q-table
q_table[state][action_index] = q_table[state][action_index] + ALPHA * (
reward + GAMMA * np.max(q_table[next_state]) - q_table[state][action_index]
)
# 更新当前状态
state = next_state
# 返回训练好的 Q-table
return q_table
q_learning()
启动我们的程序训练 100 次之后可以发现其实可以很好的进行游戏了:
深度强化学习 DQN
在上面我们讲了在 Q-learning 算法中我们以矩阵的方式建立了一张存储每个状态下所有动作 Q 值的表格。表格中的每一个动作价值 Q(s,a)表示在状态下选择动作然后继续遵循某一策略预期能够得到的期望回报。
然而,这种用表格存储动作价值的做法只在环境的状态和动作都是离散的,并且空间都比较小的情况下适用,如果是状态或者动作数量非常大的时候,这种做法就不适用了。
值函数近似(Function Approximation)的方法就是为了解决状态空间过大,通过用函数而不是 Q 表来表示 Q(s,a)。
其中 w 称为权重,也就是我们在神经网络里面需要训练收敛的值,在上面的 Q-learning 中我们的强化学习是训练 Q 表,在神经网络里面训练收敛的就是 w 值。通过神经网络和 Q-learning 结合就是 DQN(Deep Q-Network)了。
在 Q-learning 中我们更新 Q 表是利用每步的 reward 和当前 Q 表来迭代的,那么同样我们也可以用这种方法来设计我们的 Loss Function:
上面的公式其实就是一个均方误差,真实值与预测值之间的差的平方,和我们上面的 Q-learning 时序差分(temporal difference,TD)函数其实很像。
有了上面的公式之后我们就可以像 Q-learning 一样利用四元组 来训练我们的模型了。但是在一般的有监督学习中,假设训练数据是独立同分布的,我们每次训练神经网络的时候从训练数据中随机采样一个或若干个数据来进行梯度下降,随着学习的不断进行,每一个训练数据会被使用多次。
为了更好地将 Q-learning 和深度神经网络结合,DQN 算法采用了经验回放(experience replay)方法,具体做法为维护一个回放缓冲区,将每次从环境中采样得到的四元组数据存储到回放缓冲区中,训练 Q 网络的时候再从回放缓冲区中随机采样若干数据来进行训练。
因此在更新网络参数的同时目标也在不断地改变,这非常容易造成神经网络训练的不稳定性,DQN 便使用了目标网络和训练网络一起。
训练网络 用于计算原来的损失函数中 第二项,使用正常梯度下降方法来进行更新;
目标网络 用于计算原来的损失函数中 第一项,其中 表示目标网络中的参数,为了让更新目标更稳定,目标网络并不会每一步都更新。目标网络使用训练网络的一套较旧的参数每隔 C 步才会与训练网络同步一次,即 。
具体流程如下:
用随机的网络参数 初始化训练网络和目标网络; 初始化经验回放池 R; for 序列 e = 1->E do 根据训练网络 用 ε -Greedy 策略选择动作 执行动作 ,获得回报 ,环境状态变为 将 存储进回放池 R 中; 若 R 中数据足够,从中采样 N 个数据; 对每个数据,用目标网络计算 ; 最小化目标损失 ,,以此更新训练网络; 更新目标网络; 获取环境初始状态 s1; for 时间步 t= 1->T do
我们以 CartPole 为例来讲解一下 DQN 的代码。
对于 CartPole 来说输出主要由四个:
| Num | Observation | Min | Max |
|---|---|---|---|
| 0 | Cart 位置 | -4.8 | 4.8 |
| 1 | Cart 速度 | -Inf | Inf |
| 2 | Pole 角度 | ~ -0.418 rad (-24°) | ~ 0.418 rad (24°) |
| 3 | Pole 角速度 | -Inf | Inf |
行动也只有两个,向左或向右,所以我们的模型也可以构建的很简单。下面来看看具体的代码,代码也是用 chatgpt 生成的,我稍微改了一下。我们的 DQN 的网络模型采用一层 128 个神经元的全连接并以 ReLU 作为激活函数,由于游戏不是很复杂所以选用简单的两层网络结构就行了:
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import random
import gymnasium as gymclass DQN(nn.Module):
def __init__(self, input_dim, output_dim):
super(DQN, self).__init__()
self.fc1 = nn.Linear(input_dim, 128)
self.fc2 = nn.Linear(128, output_dim)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = self.fc2(x)
return x
# 超参数
num_episodes = 2000 #循环次数
current_epoch = 0 #目前循环的次数
learning_rate = 0.001 #学习率
gamma = 0.99 # 折扣因子
epsilon_start = 1.0 # epsilon-贪婪策略 开始值
epsilon_end = 0.01 # epsilon-贪婪策略 最小值
epsilon_decay = 0.995 # epsilon-贪婪策略 下降值
# 创建环境
env = gym.make("CartPole-v1", render_mode="rgb_array")
# 初始化DQN模型
input_dim = env.observation_space.shape[0]
output_dim = env.action_space.n
# 初始化训练网络
model = DQN(input_dim, output_dim)
# 设置优化器
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
# 加载上次训练的参数
if os.path.exists("model.pth"):
checkpoint = torch.load("model.pth")
model.load_state_dict(checkpoint['net'])
optimizer.load_state_dict(checkpoint['optimizer'])
current_epoch = checkpoint["epoch"]
print("load succ")
# 初始化目标网络
target_model = DQN(input_dim, output_dim)
target_model.load_state_dict(model.state_dict())
我们还需要一个缓存区来存放从环境中采样的数据:
class ReplayBuffer:
''' 经验回放池 '''
def __init__(self, capacity):
self.buffer = collections.deque(maxlen=capacity) # 队列,先进先出 def add(self, state, action, reward, next_state, done): # 将数据加入buffer
self.buffer.append((state, action, reward, next_state, done))
def sample(self, batch_size): # 从buffer中采样数据,数量为batch_size
transitions = random.sample(self.buffer, batch_size)
state, action, reward, next_state, done = zip(*transitions)
return np.array(state), action, reward, np.array(next_state), done
def size(self):
return len(self.buffer)
然后就是我们的训练函数,批量从缓存区获取数据,使用 DQN 算法进行训练:
def train(replay_buffer, batch_size):
if replay_buffer.size() < batch_size:
return
# 批量获取参数
states, actions, rewards, next_states, dones = replay_buffer.sample(batch_size) states = torch.tensor(states, dtype=torch.float)
actions = torch.tensor(actions).view(-1, 1)
rewards = torch.tensor(rewards, dtype=torch.float).view(-1, 1)
next_states = torch.tensor(next_states, dtype=torch.float)
dones = torch.tensor(dones, dtype=torch.float).view(-1, 1)
# 训练网络 Q 值
q_values = model(states).gather(1, actions)
# 目标网络 Q 值
next_q_values = target_model(next_states).max(1)[0].view(-1, 1)
target_q_values = rewards + gamma * next_q_values * (1 - dones) # TD误差目标
loss = torch.mean(torch.nn.functional.mse_loss(q_values, target_q_values)) # 均方误差损失函数
optimizer.zero_grad() # PyTorch中默认梯度会累积,这里需要显式将梯度置为0
loss.backward() # 反向传播更新参数
optimizer.step()
最后就是我们的主循环函数了,在每个 episode 中,我们选择一个动作(使用 ε-greedy 策略),执行该动作,并将结果存储在 replay buffer 中:
# 主循环
replay_buffer = ReplayBuffer(10000)
epsilon = epsilon_start
batch_size = 64
bestReward = 500
for episode in range(current_epoch,num_episodes):
state,_ = env.reset()
done = False
episode_reward = 0 while not done:
# 选择动作
if random.random() < epsilon:
action = env.action_space.sample()
else:
state_tensor = torch.FloatTensor(state)
q_values = model(state_tensor)
action = torch.argmax(q_values).item()
# 执行动作
next_state, reward, done,_, _ = env.step(action)
if reward>bestReward:
bestReward = reward
# 添加经验到replay buffer
replay_buffer.add(state, action, reward, next_state, done)
# 更新状态
state = next_state
episode_reward += reward
# 训练DQN
train(replay_buffer, batch_size)
# 更新目标网络
if episode % 10 == 0:
target_model.load_state_dict(model.state_dict())
if reward > bestReward: #保存已训练好的参数和优化器
print("save cart")
state_dict = {"net": target_model.state_dict(), "optimizer": optimizer.state_dict(), "epoch": episode}
torch.save(state_dict, "model.pth")
# 更新epsilon
epsilon = max(epsilon_end, epsilon * epsilon_decay)
print(f"Episode {episode}, Reward: {episode_reward}")
env.close()
训练完之后使用保存好的 model.pth 参数,就可以实际使用起来了:
# 创建环境
env = gym.make("CartPole-v1", render_mode="human")
# env = gym.make("CartPole-v1", render_mode="rgb_array")
# 初始化DQN模型
input_dim = env.observation_space.shape[0]
output_dim = env.action_space.n# 初始化训练网络
model = DQN(input_dim, output_dim)
if os.path.exists("model.pth"):
checkpoint = torch.load("model.pth")
model.load_state_dict(checkpoint['net'])
print("load succ")
state,_ = env.reset()
done = False
while not done:
state_tensor = torch.FloatTensor(state)
q_values = model(state_tensor)
action = torch.argmax(q_values).item()
# 执行动作
next_state, reward, done, _, _ = env.step(action)
state = next_state
总结
这一篇文章我们从最开始的 K 臂老虎机入手讲解了强化学习的基本原理,然后切入到 Q-learning 中学习如何使用 Q 表来进行强化学习,最后再借助神经网络将 Q 表替换成用函数来拟合计算 Q 值。
Reference
https://lilianweng.github.io/posts/2018-01-23-multi-armed-bandit/
https://yaoyaowd.medium.com/%E4%BB%8Ethompson-sampling%E5%88%B0%E5%A2%9E%E5%BC%BA%E5%AD%A6%E4%B9%A0-%E5%86%8D%E8%B0%88%E5%A4%9A%E8%87%82%E8%80%81%E8%99%8E%E6%9C%BA%E9%97%AE%E9%A2%98-23a48953bd30
https://zh.wikipedia.org/wiki/%E8%92%99%E5%9C%B0%E5%8D%A1%E7%BE%85%E6%96%B9%E6%B3%95
https://rl.qiwihui.com/zh_CN/latest/partI/index.html
https://github.com/ty4z2008/Qix/blob/master/dl.md
https://hrl.boyuai.com/
http://zh.d2l.ai/
如有侵权请联系:admin#unsafe.sh