别忘了 星标我!●常见加密技术●目前发现的比较常见的密钥加密技术有RC4以及TEA系列加密TEATEA(Tiny Encryption Algorithm,小型加密算法)是一种对称密钥加密算法,由英 2023-3-8 09:49:28 Author: 格格巫和蓝精灵(查看原文) 阅读量:42 收藏
目前发现的比较常见的密钥加密技术有RC4以及TEA系列加密
TEA(Tiny Encryption Algorithm,小型加密算法)是一种对称密钥加密算法,由英国计算机科学家David Wheeler和Roger Needham在1994年提出。TEA算法以64位(8字节)的块大小和128位(16字节)的密钥长度为特点,它可以用于加密和解密数据,同时具有简单、高效、安全的特点。
TEA算法的加密和解密操作都是基于一个32轮迭代的加密算法,每一轮都是对明文和密钥进行加密运算,然后将运算结果作为下一轮的输入,最后输出密文。TEA算法的加密和解密过程是相同的,因此它是一种对称密钥加密算法。TEA算法的安全性取决于密钥长度,因为密钥越长,破解难度越大。
尽管TEA算法是一种简单的加密算法,但它已经被广泛应用于各种安全领域,例如网络通信、软件保护、数字版权保护、金融交易等。同时,由于TEA算法的加密过程非常简单,因此它可以在资源受限的设备上使用,如智能卡、嵌入式系统、移动设备等。
详细加密流程
TEA(Tiny Encryption Algorithm)算法是一种对称密钥加密算法,它使用相同的密钥进行加密和解密。TEA算法的加密流程如下:
1. 将明文按64位(8字节)分组,将每个分组视为一个64位的二进制数,记为V。
2. 将128位的密钥分成4个32位的子密钥,分别记为K0、K1、K2、K3。
3. 将明文分组V分为两个32位的部分,分别记为V0和V1。
4. 设定一个32位的常数delta,其值为0x9E3779B9。
5. TEA算法的加密过程包括32轮迭代,每一轮的加密过程如下:
a. 首先,累加器sum被初始化为0。
sum += delta;v0 += ((v1 << 4) + k[0]) ^ (v1 + sum) ^ ((v1 >> 5) + k[1]);v1 += ((v0 << 4) + k[2]) ^ (v0 + sum) ^ ((v0 >> 5) + k[3]);
6. 经过32轮迭代后,得到加密后的密文,记为C0和C1。
7. 将C0和C1按顺序连接起来,得到64位的密文。
TEA算法的解密过程与加密过程基本相同,只是将加密过程中的加法操作改为减法操作,将右移操作改为左移操作。具体过程如下:
1. 将密文按64位(8字节)分组,将每个分组视为一个64位的二进制数,记为C。
2. 将128位的密钥分成4个32位的子密钥,分别记为K0、K1、K2、K3。
3. 将密文分组C分为两个32位的部分,分别记为C0和C1。
4. 设定一个32位的常数delta,其值为0x9E3779B9。
5. TEA算法的解密过程也包括32轮迭代,每一轮的解密过程如下:
v1 -= ((v0 << 4) + k[2]) ^ (v0 + sum) ^ ((v0 >> 5) + k[3]);v0 -= ((v1 << 4) + k[0]) ^ (v1 + sum) ^ ((v1 >> 5) + k[1]);sum -= delta;//sum的值为delta乘以加密时的迭代次数
6. 最后,经过32轮迭代加密后,得到的V0和V1拼接在一起,形成64位(8字节)的密文。
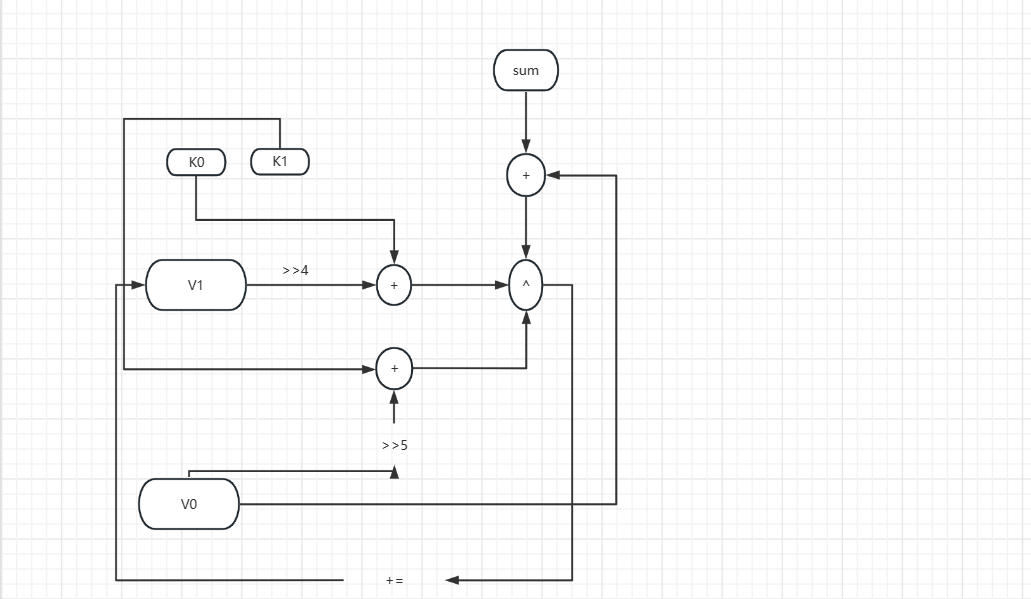
流程图
这里只展示对v1操作的流程,v2操作与如下流程一致,只是更换了key的值,其中每次sum还需要加一次delta的值。
解密过程亦是如此,每一次都是减delta的值。
代码
#include <stdio.h>#include <stdint.h> // 使用uint32_t数据类型需要包含此头文件#include <string.h>// 定义加密函数void tea_encrypt(uint32_t *v, uint32_t *k) {uint32_t v0 = v[0], v1 = v[1], sum = 0, i;uint32_t delta = 0x9e3779b9;for (i = 0; i < 32; i++) {sum += delta;v0 += ((v1 << 4) + k[0]) ^ (v1 + sum) ^ ((v1 >> 5) + k[1]);v1 += ((v0 << 4) + k[2]) ^ (v0 + sum) ^ ((v0 >> 5) + k[3]);}v[0] = v0;v[1] = v1;}// 定义解密函数void tea_decrypt(uint32_t *v, uint32_t *k) {uint32_t v0 = v[0], v1 = v[1], sum = 0xC6EF3720, i; // 根据TEA算法,解密轮次的计算需要初始化sumuint32_t delta = 0x9e3779b9;for (i = 0; i < 32; i++) {v1 -= ((v0 << 4) + k[2]) ^ (v0 + sum) ^ ((v0 >> 5) + k[3]);v0 -= ((v1 << 4) + k[0]) ^ (v1 + sum) ^ ((v1 >> 5) + k[1]);sum -= delta;}v[0] = v0;v[1] = v1;}// 定义测试函数void test_tea(const char *plaintext, const char *key) {printf("TEA加密算法\n");printf("原始明文:\t%s\n", plaintext);printf("密钥:\t\t%s\n", key);// 将明文按照64位分组uint32_t blocks[2]; // 两个32位的块,即64位memcpy(blocks, plaintext, 8);// 将密钥按照64位分组uint32_t key_blocks[4]; // 四个32位的块,即128位memcpy(key_blocks, key, 16);// 加密tea_encrypt(blocks, key_blocks);// 将加密后的结果输出printf("加密后的密文:\t%08x%08x\n", blocks[0], blocks[1]);// 解密tea_decrypt(blocks, key_blocks);// 将解密后的结果输出char decrypted[9];memcpy(decrypted, blocks, 8);decrypted[8] = '\0';printf("解密后的明文:\t%s\n", decrypted);}int main() {test_tea("Hello, world!", "This is a key.");//由于tea算法一次只能加密解密16个byte位的数据,所以此处数据丢失return 0;}
逆向原理以及常见问题
在逆向中,由于tea加密的特性,每次都是两个两个值一起加密,所以通常出题人会将四个字符合并成为一个大整数
类似于abcd字符串,需要加密时出题者会将其写为0x64636261(小端序存储)
编写一段简单的tea代码
#include <stdint.h>#include<stdio.h>void tea_encrypt(uint32_t* v, uint32_t* k) {uint32_t sum = 0;uint32_t delta = 0x9e3779b9;uint32_t v0 = v[0], v1 = v[1];uint32_t k0 = k[0], k1 = k[1], k2 = k[2], k3 = k[3];for (int i = 0; i < 32; i++) {sum += delta;v0 += ((v1 << 4) + k0) ^ (v1 + sum) ^ ((v1 >> 5) + k1);v1 += ((v0 << 4) + k2) ^ (v0 + sum) ^ ((v0 >> 5) + k3);}v[0] = v0;v[1] = v1;}void tea_decrypt(uint32_t* v, uint32_t* k) {uint32_t sum = 0xC6EF3720;uint32_t delta = 0x9e3779b9;uint32_t v0 = v[0], v1 = v[1];uint32_t k0 = k[0], k1 = k[1], k2 = k[2], k3 = k[3];for (int i = 0; i < 32; i++) {v1 -= ((v0 << 4) + k2) ^ (v0 + sum) ^ ((v0 >> 5) + k3);v0 -= ((v1 << 4) + k0) ^ (v1 + sum) ^ ((v1 >> 5) + k1);sum -= delta;}v[0] = v0;v[1] = v1;}int main() {uint32_t plaintext[4] = {0x64636261, 0x68676665,0x6C6B6A69,0x706F6E6D};uint32_t key[4] = {0x12345678, 0x9abcdef0, 0xfedcba98, 0x76543210};uint32_t enc[4]={0};for(int i=0 ; i<4 ; i+=2 ){tea_encrypt(plaintext+i,key);}for(int i = 0 ; i < 4 ; i+=2 ){tea_decrypt(plaintext + i , key);}printf("%s",plaintext);return 0;}
我们查看他在ida中的反汇编代码
tea加密步骤
解密步骤也在一开始的代码中,其中也有不是两两一组进行加密的,也可以是叠加加密,再解密过程中需要稍作处理,具体在XTEA的例题中讲解。
如果按照这种模式出题,解密函数已经在源程序中给出。但是这种tea的在日常解题中是比较baby的算法,其中有一些对key值做处理的题目需要特别注意,具体会在XTEA中展示。
在tea算法中还有需要注意的点就是delta值并不是仅限于黄金比例,其值是可以变换的而且不论正数负数。
XTEA算法(eXtended Tiny Encryption Algorithm)是TEA算法的一种改进,它是一种块密码算法,采用64位密钥和64位分组。XTEA算法的安全性比TEA算法更高,同时加密/解密速度也更慢。
XTEA算法的加密和解密过程类似于TEA算法,只是使用了不同的轮函数,加密和解密过程如下:
1. 将明文按64位(8字节)分组,将每个分组视为一个64位的二进制数,记为V。
2. 将64位密钥分为4个32位子密钥,记为K0、K1、K2、K3。
3. 将V分为两个32位的半块V0和V1。
4. 初始化轮密钥sum为0。
5. 执行32轮迭代,每轮迭代包括以下操作:
V0 += (((V1 << 4) ^ (V1 >> 5)) + V1) ^ (sum + K[sum & 3])
sum += delta
V1 += (((V0 << 4) ^ (V0 >> 5)) + V0) ^ (sum + K[(sum >> 11) & 3])
6. 将迭代后的V0和V1合并为64位的加密结果。
XTEA算法和TEA算法一样,被广泛应用于网络通信、数据加密等领域。
XTEA与TEA的区别
TEA算法和XTEA算法都是块密码算法,都是对称密钥算法,它们的主要区别在于轮函数的不同。TEA算法的轮函数中只有简单的加、减、异或等运算,而XTEA算法的轮函数中包含了更多的运算,例如位运算、循环移位等。
具体来说,XTEA算法将TEA算法的轮函数改为:
v0 += (((v1 << 4) ^ (v1 >> 5)) + v1) ^ (sum + key[(sum >> 11) & 3]);v1 += (((v0 << 4) ^ (v0 >> 5)) + v0) ^ (sum + key[sum & 3]);
XTEA算法在TEA算法的基础上进行了改进,主要改进有以下几点:
1. 增加了迭代轮数:TEA算法迭代轮数为32轮,XTEA算法增加到了64轮,加强了加密强度。
2. 改进了密钥扩展算法:XTEA算法的密钥扩展算法相对于TEA算法更为复杂和高效。
3. 加入了反向迭代:XTEA算法加入了反向迭代,即加密和解密的过程完全相同。
4. 可变的块大小:XTEA算法的块大小可变,可以是64位、128位等多种长度,提供了更加灵活的加密选项。
5. 增加了数据完整性保护:XTEA算法可以通过增加MAC(Message Authentication Code)来保护数据完整性,防止数据在传输过程中被篡改。
综上所述,XTEA算法相对于TEA算法在安全性、效率和功能性等方面都有所提高,因此被广泛应用于加密通信、数字签名、数据完整性保护等领域。
常见题型:
[Hgame]VidarCamera
private final int[] m41encrypthkIa6DI(int[] iArr) { int i;int[] r1 = UIntArray.m208constructorimpl(4);UIntArray.m219setVXSXFK8(r1, 0, 2233);UIntArray.m219setVXSXFK8(r1, 1, 4455);UIntArray.m219setVXSXFK8(r1, 2, 6677);UIntArray.m219setVXSXFK8(r1, 3, 8899);int i2 = 0;while (i2 < 9) {int i3 = 0;int i4 = 0;do {i3++;i = i2 + 1;UIntArray.m219setVXSXFK8(iArr, i2, UInt.m155constructorimpl(UIntArray.m214getpVg5ArA(iArr, i2) + UInt.m155constructorimpl(UInt.m155constructorimpl(UInt.m155constructorimpl(UIntArray.m214getpVg5ArA(r1, UInt.m155constructorimpl(i4 & 3)) + i4) ^ UInt.m155constructorimpl(UInt.m155constructorimpl(UInt.m155constructorimpl(UIntArray.m214getpVg5ArA(iArr, i) << 4) ^ UInt.m155constructorimpl(UIntArray.m214getpVg5ArA(iArr, i) >>> 5)) + UIntArray.m214getpVg5ArA(iArr, i))) ^ i4)));UIntArray.m219setVXSXFK8(iArr, i, UInt.m155constructorimpl(UIntArray.m214getpVg5ArA(iArr, i) + UInt.m155constructorimpl(UInt.m155constructorimpl(UInt.m155constructorimpl(UInt.m155constructorimpl(UIntArray.m214getpVg5ArA(iArr, i2) << 4) ^ UInt.m155constructorimpl(UIntArray.m214getpVg5ArA(iArr, i2) >>> 5)) + UIntArray.m214getpVg5ArA(iArr, i2)) ^ UInt.m155constructorimpl(UIntArray.m214getpVg5ArA(r1, UInt.m155constructorimpl(UInt.m155constructorimpl(i4 >>> 11) & 3)) + i4))));i4 = UInt.m155constructorimpl(i4 + 878077251);} while (i3 <= 32);i2 = i;}return iArr;}
这种题的代码写的非常的复杂,但是根据tea的特征可以发现key以及delta值。但是这里比较坑的地方是i2这部分是<9的那么也就是他是单数次循环,可是我们常见的tea是两两一组循环加密的,这是怎么回事呢。
这就是涉及到了一个叠加加密的方式。
例如有五个值v1,v2,v3,v4,v5那么我可以先将v1,v2加密,然后再拿加密后的v2与v3加密这样循环
因此如果我们还按照传统的tea两组两组解密的方法的话,就会导致v2的值与v2和v1加密时的值不一样了,就会导致从前向后无法正常解密回去,因此需要从v5,v4开始解密。
该题的解密脚本为:
#include<iostream>#include<algorithm>#include<cstdio>#include<cmath>#include<map>#include<vector>#include<queue>#include<stack>#include<set>#include<string>#include<cstring>#include<list>#include<stdlib.h>using namespace std;typedef int status;typedef int selemtype;#include <stdio.h>#include <stdint.h>void m41encrypthkIa6DI(unsigned int iArr[]) {int i;unsigned int r1[4] = {2233, 4455, 6677, 8899};int i2 = 0;int i3 = 0;unsigned int i4 = 0;int a1 = iArr[0];int a2 = iArr[1];for(int i = 0 ; i <= 32 ; i++ ){i4+=878077251;}do {i3++;i = i2 + 1;i4 = i4 - 878077251;iArr[i] -= (unsigned int)( ((unsigned int)(iArr[i2] << 4 )^ (unsigned int)(iArr[i2] >> 5) )+ iArr[i2] ) ^ (unsigned int)(r1[(i4 >> 11) & 3] + i4);iArr[i2] -= (unsigned int)( (unsigned int)(r1[i4 & 3] + i4) ^ (unsigned int)((unsigned int)( (iArr[i] << 4) ^ (unsigned int)(iArr[i] >> 5) ) + iArr[i] ))^ i4;} while (i3 <= 32);i2 = i;}unsigned int flag[11]={0};int main (){flag[0]=637666042;flag[1]=457511012;flag[2]=-2038734351;flag[3]=578827205;flag[4]=-245529892;flag[5]=-1652281167;flag[6]=435335655;flag[7]=733644188;flag[8]=705177885;flag[9]=-596608744;for(int i = 8 ; i >= 0 ; i -- ){m41encrypthkIa6DI(flag+i);}for(int i = 0 ; i < 10 ; i ++ ){printf("%x,",flag[i]);}cout<<endl;// printf("\n%c\n",0x5a);printf("%s\n",flag);}
[[HNCTF 2022 WEEK2]TTTTTTTTTea]
该题加密部分:
__int64 __fastcall tea_encrypt(unsigned int *a1, __int64 a2){__int64 result; // raxunsigned __int64 i; // [rsp+8h] [rbp-18h]unsigned int v4; // [rsp+14h] [rbp-Ch]unsigned int v5; // [rsp+18h] [rbp-8h]unsigned int v6; // [rsp+1Ch] [rbp-4h]v6 = *a1;v5 = a1[1];v4 = 0;for ( i = 0i64; i <= 0x1F; ++i ){v6 += (((v5 >> 5) ^ (16 * v5)) + v5) ^ (*(_DWORD *)(4i64 * (v4 & 3) + a2) + v4);v4 -= 1640531527;v5 += (((v6 >> 5) ^ (16 * v6)) + v6) ^ (*(_DWORD *)(4i64 * ((v4 >> 11) & 3) + a2) + v4);}*a1 = v6;result = v5;a1[1] = v5;return result;}
可以发现这显然是一道tea加密的题目,为XTEA。这里需要讲解的是tea常见的key存储方式,我们在ida中可以看到该题key存储方式
可以发现正常的tea存储key的方式只有4个数字,而该处出现了16位数字,其实在开头的介绍中说过key是由128bit组成的,分割成为四份32bit的值,那么我们可以看到ida中这里的一个数字为2byte也就是8bit那么我们需要取四位数字,然后由于小端序存储的问题,类似于该题则我们应该写的是0x00010203,0x04050607,0x08090A0B,0x0C0D0E0F。就是我们需要使用的key值。
该题的解密脚本此处就不贴出了,只是讲讲这种典型的key值存取问题。tea的考点基本如此.
RC4是一种流密码算法,由Ron Rivest于1987年设计。RC4的名字源于它是“Rivest Cipher 4”的缩写。
RC4算法使用变量长度的密钥来生成伪随机比特流,该比特流可以与明文进行异或运算得到密文。RC4算法的特点是简单高效,适用于低带宽的网络通信。
RC4算法的核心是密钥调度算法(Key Scheduling Algorithm,KSA)和伪随机生成算法(Pseudo-Random Generation Algorithm,PRGA)。密钥调度算法将密钥按字节分成256个元素的S盒,然后对S盒进行混淆和置换,生成256个随机排列的字节,即密钥调度表。伪随机生成算法则使用密钥调度表和一个计数器来生成伪随机比特流。
RC4算法的加密过程如下:
1. 初始化:创建一个256字节的S盒,使用密钥调度算法生成密钥调度表,并初始化计数器。
2. 生成伪随机比特流:使用密钥调度表和计数器生成伪随机比特流。
3. 明文加密:将明文与伪随机比特流进行异或运算得到密文。
4. 重复步骤2和3:使用相同的密钥和初始化向量对每个数据块重复执行步骤2和3。
RC4算法的解密过程与加密过程相同,因为异或运算是可逆的。
需要注意的是,RC4算法的密钥长度不应太短,否则容易受到攻击。通常建议使用长度为128位或以上的密钥。此外,RC4算法在初始化时需要避免使用相同的密钥和初始化向量,否则会导致生成的伪随机比特流重复,从而降低加密强度。
关键变量
1. 密钥流:RC4算法的关键是根据明文和密钥生成相应的密钥流,密钥流的长度和明文的长度是对应的,也就是说明文的长度是500字节,那么密钥流也是500字节。当然,加密生成的密文也是500字节,因为密文第i字节=明文第i字节^密钥流第i字节;
2. 状态向量S:长度为256,S[0],S[1].....S[255]。每个单元都是一个字节,算法运行的任何时候,S都包括0-255的8比特数的排列组合,只不过值的位置发生了变换;
3. 临时向量T:长度也为256,每个单元也是一个字节。如果密钥的长度是256字节,就直接把密钥的值赋给T,否则,轮转地将密钥的每个字节赋给T;
4. 密钥K:长度为1-256字节,注意密钥的长度keylen 与明文长度、密钥流的长度没有必然关系,通常密钥的长度趣味16字节(128比特)。
三步加密
初始化S和T
int Len = strlen(key); for(i=0;i<256;i++) {s[i]=i;T[i]=key[i%Len];}
初始化排列S
for(i=0;i<256;i++) { j=(j+s[i]+k[i])%256;tmp=s[i];s[i]=s[j];//交换s[i]和s[j]s[j]=tmp;}
产生密钥流
int i=0,j=0,t=0;unsigned long k=0;unsigned char tmp;for(k=0;k < len;k++){i=(i+1)%256;j=(j+s[i])%256;tmp=s[i];s[i]=s[j]; //交换s[x]和s[y]s[j]=tmp;}
流程图
+------------++--->| Initialize || +------------+| || | (K)| v| +------------+| | Key-scheduling || +------------+| || | (P)| v| +------------++--->| Encryption |+------------+|v+------------+| Output CT |+------------+
完整加密解密程序
//程序开始#include<stdio.h>#include<string.h>typedef unsigned longULONG;/*初始化函数*/void rc4_init(unsigned char*s, unsigned char*key, unsigned long Len){int i = 0, j = 0;char k[256] = { 0 };unsigned char tmp = 0;for (i = 0; i<256; i++){s[i] = i;k[i] = key[i%Len];}for (i = 0; i<256; i++){j = (j + s[i] + k[i]) % 256;tmp = s[i];s[i] = s[j];//交换s[i]和s[j]s[j] = tmp;}}/*加解密*/void rc4_crypt(unsigned char*s, unsigned char*Data, unsigned long Len){int i = 0, j = 0, t = 0;unsigned long k = 0;unsigned char tmp;for (k = 0; k<Len; k++){i = (i + 1) % 256;j = (j + s[i]) % 256;tmp = s[i];s[i] = s[j];//交换s[x]和s[y]s[j] = tmp;t = (s[i] + s[j]) % 256;Data[k] ^= s[t];}}int main(){unsigned char s[256] = { 0 }, s2[256] = { 0 };//S-boxchar key[256] = { "justfortest" };char pData[512] = "这是一个用来加密的数据Data";unsigned long len = strlen(pData);int i;printf("pData=%s\n", pData);printf("key=%s,length=%d\n\n", key, strlen(key));rc4_init(s, (unsigned char*)key, strlen(key));//已经完成了初始化printf("完成对S[i]的初始化,如下:\n\n");for (i = 0; i<256; i++){printf("%02X", s[i]);if (i && (i + 1) % 16 == 0)putchar('\n');}printf("\n\n");for (i = 0; i<256; i++)//用s2[i]暂时保留经过初始化的s[i],很重要的!!!{s2[i] = s[i];}printf("已经初始化,现在加密:\n\n");rc4_crypt(s, (unsigned char*)pData, len);//加密printf("pData=%s\n\n", pData);printf("已经加密,现在解密:\n\n");//rc4_init(s,(unsignedchar*)key,strlen(key));//初始化密钥rc4_crypt(s2, (unsigned char*)pData, len);//解密printf("pData=%s\n\n", pData);return 0;}//程序完
常见题型以及解答
RC4的加密解密问题分为两种方式,因为我们可以发现rc4其中欧冠的初始化S,T与初始化排列S盒都是与我们需要加密的密钥无关的,最终与加密原文有关的只有最后一段的异或。因此RC4题型给出两种解答方法。
这里利用例题来讲解:[Reverse]crypt
(https://shangwendada.co/index.php/2022/11/09/reversecryptrc4/)
动态调试取异或值
我们将上文中写到的加密脚本编译后放入ida中观察。
可以看到rc4的特点就是通常使用两个加密函数,一个用来初始化S盒与T盒,另一个则用来将明文与密钥流异或。
因此我们只需要在异或处下断点然后拿出寄存器中的值与密文异或就能够解决问题。
常规脚本解法
常规脚本就是复制粘贴下题目的加密解密函数,将题目中的加密函数复制下来,然后直接使用就行,这里贴出例题中的解密脚本
#include<stdio.h>#include<windows.h>#include<cstring>using namespace std;char key[] ={0x9E, 0xE7, 0x30, 0x5F, 0xA7, 0x01, 0xA6, 0x53, 0x59, 0x1B,0x0A, 0x20, 0xF1, 0x73, 0xD1, 0x0E, 0xAB, 0x09, 0x84, 0x0E,0x8D, 0x2B, 0x00, 0x00};char Str[]="12345678abcdefghijklmnopqrspxyz";__int64 __fastcall sub_140001120(DWORD *a1, char *a2, int a3){__int64 result; // raxint i; // [rsp+0h] [rbp-28h]int j; // [rsp+0h] [rbp-28h]int v6; // [rsp+4h] [rbp-24h]int v7; // [rsp+8h] [rbp-20h]int v8; // [rsp+Ch] [rbp-1Ch]DWORD *v9; // [rsp+10h] [rbp-18h]*a1 = 0;a1[1] = 0;v9 = a1 + 2;for ( i = 0; i < 256; ++i )v9[i] = i;v6 = 0;result = 0;v7 = 0;for ( j = 0; j < 256; ++j ){v8 = v9[j];v7 = (unsigned __int8)(*(BYTE *)(a2 + v6) + v8 + v7);v9[j] = v9[v7];v9[v7] = v8;if ( ++v6 >= a3 )v6 = 0;result = (unsigned int)(j + 1);}return result;}DWORD sub_140001240(DWORD *a1, char* a2, int a3){DWORD *result; // raxint i; // [rsp+0h] [rbp-28h]int v5; // [rsp+4h] [rbp-24h]int v6; // [rsp+8h] [rbp-20h]int v7; // [rsp+Ch] [rbp-1Ch]int v8; // [rsp+10h] [rbp-18h]DWORD *v9; // [rsp+18h] [rbp-10h]v5 = *a1;v6 = a1[1];v9 = a1 + 2;for ( i = 0; i < a3; ++i ){v5 = (unsigned __int8)(v5 + 1);v7 = v9[v5];v6 = (unsigned __int8)(v7 + v6);v8 = v9[v6];v9[v5] = v8;v9[v6] = v7;*(BYTE *)(a2 + i) ^= LOBYTE(v9[(unsigned __int8)(v8 + v7)]);}*a1 = v5;result = a1;a1[1] = v6;}int i;int main(){DWORD *v9;v9=(DWORD *)malloc(0x408*sizeof(v9));sub_140001120(v9,Str,strlen(Str));for(int i = 0 ; i < strlen(key);i ++ ){key[i]^=34;}sub_140001240(v9,key,strlen(key));printf("%s",key);}
注意
RC4出题中,伪比特流的产生方法不唯一,也就是说S盒与T盒的制作方法不会唯一,存在较大的魔改空间。
[由于该加密方式考的比较少,此处不深入研究]
ChaCha20是一种流密码算法,用于加密和解密数据流。它由Daniel J. Bernstein于2008年设计,是Salsa20的改进版,被广泛应用于网络通信、加密文件和存储介质等领域。
ChaCha20算法使用256位的密钥和一个12字节的随机数(称为nonce)作为输入,生成一个可变长度的伪随机比特流,然后与明文进行异或运算得到密文。ChaCha20算法的特点是快速、安全、易于实现和内存友好,适用于高速网络通信和移动设备。
与RC4的区别
眼尖的可能发现了,chacha20也是使用伪随机比特流来产生密钥的,然后将密钥与明文异或进行加密,接下来就讲讲他们在安全性下的区别吧。
Chacha20和RC4都是流密码算法,但它们的加密原理有以下几个区别:
1. 密钥长度:Chacha20的密钥长度为256位(32字节),而RC4的密钥长度为1到256字节不等。因此,Chacha20可以提供更强的密钥安全性,也更适合用于现代加密应用。
2. S盒:Chacha20没有S盒,而RC4使用一个256字节的S盒来生成密钥流。Chacha20是基于置换的加密算法,它使用固定的置换来生成密钥流。
3. 加密过程:在Chacha20中,通过对输入的明文数据块进行置换和加密操作,生成密文输出。每次加密需要根据密钥和计数器生成一个新的置换和密钥流。而RC4是在密钥生成完毕后,直接用密钥流对输入的明文进行异或操作得到密文输出。
4. 安全性:由于RC4存在一些安全性问题,它已经不被推荐使用。而Chacha20已经被广泛应用于TLS、SSH、IPsec等加密通信协议中,并且其安全性得到了广泛认可。
综上所述,Chacha20相比于RC4,具有更高的密钥安全性和更好的安全性保障,更加适合用于现代加密应用。
加密步骤
ChaCha20算法的加密过程如下:
1. 初始化:使用密钥和随机数生成初始状态。
2. 生成伪随机比特流:使用初始状态和计数器生成伪随机比特流。
3. 明文加密:将明文与伪随机比特流进行异或运算得到密文。
4. 重复步骤2和3:使用相同的密钥和随机数对每个数据块重复执行步骤2和3。
ChaCha20算法的解密过程与加密过程相同,因为异或运算是可逆的。
需要注意的是,ChaCha20算法的密钥长度不应太短,否则容易受到攻击。通常建议使用长度为256位的密钥。此外,随机数在每次使用时应该是不同的,否则会导致生成的伪随机比特流重复,从而降低加密强度。
以下是一个使用Python 3实现ChaCha20加密的示例脚本:
import structimport hashlibdef chacha20_encrypt(key, nonce, plaintext):# 生成初始状态state = [0x61707865, 0x3320646e, 0x79622d32, 0x6b206574]state += struct.unpack('<4I', key)state += [0] * 4state += struct.unpack('<3I', nonce) + [0]# 生成伪随机比特流def quarterround(a, b, c, d):state[a] += state[b]state[d] ^= state[a]state[d] = (state[d] << 16) | (state[d] >> 16)state[c] += state[d]state[b] ^= state[c]state[b] = (state[b] << 12) | (state[b] >> 20)state[a] += state[b]state[d] ^= state[a]state[d] = (state[d] << 8) | (state[d] >> 24)state[c] += state[d]state[b] ^= state[c]state[b] = (state[b] << 7) | (state[b] >> 25)buf = bytearray(plaintext)for i in range(0, len(buf), 64):x = state[:]for j in range(10):quarterround(0, 4, 8, 12)quarterround(1, 5, 9, 13)quarterround(2, 6, 10, 14)quarterround(3, 7, 11, 15)quarterround(0, 5, 10, 15)quarterround(1, 6, 11, 12)quarterround(2, 7, 8, 13)quarterround(3, 4, 9, 14)for j in range(16):x[j] += state[j]buf[i+j] ^= (x[j] & 0xff)buf[i+j+1:i+j+4] = bytes([((x[j] >> k) & 0xff) for k in (8, 16, 24)])return bytes(buf)# 示例用法key = hashlib.sha256(b'my secret key').digest()nonce = b'\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00'plaintext = b'hello world'ciphertext = chacha20_encrypt(key, nonce, plaintext)print(ciphertext.hex())
该脚本中的chacha20_encrypt函数接收密钥、随机数和明文作为输入,返回加密后的密文。实现中使用了Python标准库中的struct模块和bytearray类型来处理二进制数据。
例题
为什么这里讲到了chacha20,因为在Hgame的比赛中出现了该题,解出的人还是比较少的,这里讲讲
chacha20这里推荐直接dump密钥来进行getflag
from idaapi import get_reg_valprint(get_reg_val('ecx'),end=",")
这里使用idapython直接调取寄存器的值
解密脚本就是如下:
int main(){unsigned int key[] = {1077387342,4258923078,1013905953,3483163055,1731413945,233590496,327206097,984787250,39669927,2202679682};unsigned char v2[40];v2[0] = 0x28;v2[1] = 0x50;v2[2] = -63;v2[3] = 35;v2[4] = -104;v2[5] = -95;v2[6] = 65;v2[7] = 54;v2[8] = 76;v2[9] = 49;v2[10] = -53;v2[11] = 82;v2[12] = -112;v2[13] = -15;v2[14] = -84;v2[15] = -52;v2[16] = 15;v2[17] = 108;v2[18] = 42;v2[19] = -119;v2[20] = 127;v2[21] = -33;v2[22] = 17;v2[23] = -124;v2[24] = 127;v2[25] = -26;v2[26] = -94;v2[27] = -32;v2[28] = 89;v2[29] = -57;v2[30] = -59;v2[31] = 70;v2[32] = 93;v2[33] = 41;v2[34] = 56;v2[35] = -109;v2[36] = -19;v2[37] = 21;v2[38] = 122;v2[39] = -1;for (int i = 0; i < 10; i++){putchar(v2[i*4 + 0] ^ (key[i] >> 24));putchar(v2[i*4 + 1] ^ (key[i] >> 16));putchar(v2[i*4 + 2] ^ (key[i] >> 8));putchar(v2[i*4 + 3] ^ (key[i] >> 0));}}
由于比较简单,这里不深入研究
ROT加密,也称为“字母位移加密”或“移位加密”,是一种简单的加密算法。它通过将明文中的每个字母按照一定规则进行移位操作来生成密文,常用于简单的加密需求或者编码中。
ROT加密的原理非常简单,只需要将明文中的每个字母按照一定的规则向右移动指定的位数,得到对应的密文。具体来说,如果移位数为N,则明文中的字母A会被替换成第N个字母,B会被替换成第N+1个字母,以此类推。如果移位数为26(即字母表的总长度),则加密后的密文就是明文的一种循环置换。
ROT加密算法的弱点在于它的加密过程非常简单,容易被破解。而且,ROT加密算法只适用于纯文本的加密,不适用于加密数字、二进制等其他数据类型。
举例
以下是一个简单的Python实现ROT13加密的例子:
def rot13(s):result = ''for c in s:if 'a' <= c <= 'z':result += chr((ord(c) - ord('a') + 13) % 26 + ord('a'))elif 'A' <= c <= 'Z':result += chr((ord(c) - ord('A') + 13) % 26 + ord('A'))else:result += creturn result
在这个例子中,我们将字母按照ROT13的规则进行移位操作。对于明文中的每个字母,如果它是一个小写字母,则将其移动13个位置,如果是一个大写字母,则也将其移动13个位置。对于非字母字符,我们直接将其保留。最后返回加密后的密文字符串。
BASE64属于是入门级别的东西了,这里只需要发现base64的加密解密函数就能发现base64加密
类似于下图:
换表
这里直接分享一个换表的脚本:
import base64import stringstr1 = "AMHo7dLxUEabf6Z3PdWr6cOy75i4fdfeUzL17kaV7rG=" #待解秘字符串string1 = "qaCpwYM2tO/RP0XeSZv8kLd6nfA7UHJ1No4gF5zr3VsBQbl9juhEGymc+WTxIiDK" #新表string2 = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"print (base64.b64decode(str1.translate(str.maketrans(string1,string2))))
顺便分享一个c++版本的
#include<iostream>#include<cstring>#include<bitset>#include<vector>#include<stdlib.h>#include<time.h>#include<sstream>#include<cstring>/*base64.c*/#include "base64.h"using namespace std;//base64.c#include"base64.h"char base64char[] = {'A','B','C','D','E','F','G','H','I','J','K','L','M','N','O','P','Q','R','S','T','U','V','W','X','Y','Z','a','b','c','d','e','f','g','h','i','j','k','l','m','n','o','p','q','r','s','t','u','v','w','x','y','z','0','1','2','3','4','5','6','7','8','9','+', '/', '\0'};/*char base64char[] = {'K','L','M','N','O','P','Q','R','S','T','A','B','C','D','E','F','G','H','I','J','e','f','g','h','i','j','k','l','m','n','U','V','W','X','Y','Z','a','b','c','d','o','p','q','r','s','t','u','v','w','x','y','z','0','1','2','3','4','5','6','7','8','9','+', '/', '\0'};*/char c;void Menu(){printf("***************\n");printf("*1、base64加密\n");printf("*2、base64解密\n");printf("*3、退出程序\n");printf("***************\n");}char* base64_encode(char* binData, char* base64, int binLength){int i = 0;int j = 0;int current = 0;for (i = 0; i < binLength; i += 3) {//获取第一个6位current = (*(binData + i) >> 2) & 0x3F;*(base64 + j++) = base64char[current];//获取第二个6位的前两位current = (*(binData + i) << 4) & 0x30;//如果只有一个字符,那么需要做特殊处理if (binLength <= (i + 1)) {*(base64 + j++) = base64char[current];*(base64 + j++) = '=';*(base64 + j++) = '=';break;}//获取第二个6位的后四位current |= (*(binData + i + 1) >> 4) & 0xf;*(base64 + j++) = base64char[current];//获取第三个6位的前四位current = (*(binData + i + 1) << 2) & 0x3c;if (binLength <= (i + 2)) {*(base64 + j++) = base64char[current];*(base64 + j++) = '=';break;}//获取第三个6位的后两位current |= (*(binData + i + 2) >> 6) & 0x03;*(base64 + j++) = base64char[current];//获取第四个6位current = *(binData + i + 2) & 0x3F;*(base64 + j++) = base64char[current];}*(base64 + j) = '\0';return base64;}unsigned char * base64_decode(char const* base64Str,unsigned char* debase64Str, int encodeStrLen){int i = 0;int j = 0;int k = 0;char temp[4] = "";for (i = 0; i < encodeStrLen; i += 4) {for (j = 0; j < 64; j++) {if (*(base64Str + i) == base64char[j]) {temp[0] = j;}}for (j = 0; j < 64; j++) {if (*(base64Str + i + 1) == base64char[j]) {temp[1] = j;}}for (j = 0; j < 64; j++) {if (*(base64Str + i + 2) == base64char[j]) {temp[2] = j;}}for (j = 0; j < 64; j++) {if (*(base64Str + i + 3) == base64char[j]) {temp[3] = j;}}*(debase64Str + k++) = ((temp[0] << 2) & 0xFC) | ((temp[1] >> 4) & 0x03);if (*(base64Str + i + 2) == '=')break;*(debase64Str + k++) = ((temp[1] << 4) & 0xF0) | ((temp[2] >> 2) & 0x0F);if (*(base64Str + i + 3) == '=')break;*(debase64Str + k++) = ((temp[2] << 6) & 0xF0) | (temp[3] & 0x3F);}return debase64Str;}int main(){char ad[]="wr3ClVcSw7nCmMOcHcKgacOtMkvDjxZ6asKWw4nChMK8IsK7KMOOasOrdgbDlx3DqcKqwr0hw701Ly57w63CtcOl";unsigned char add[256]={0};base64_decode(ad,add,88);for(int i = 0 ; i <88; i++ ){printf("0x%x,",add[i]);}/*for(int i = 0 ; i < strlen(base64char);i++){printf("%c",base64char[i]);}*/}
以上就是我常在ctf逆向中遇到的加密解密内容了,本篇文章偏向于新手向,内容还是比较详细的,希望能给大家带来帮助。
如有侵权请联系:admin#unsafe.sh