作者:foxxiao,腾讯 WXG 后开开发工程师本文对完美 Hash 的概念进行了梳理,通过 Hash 构建步骤来了解它是如何解决 Hash 冲突的,并比较了 Hash 表和完美 Hash 表。下面 2022-7-20 18:3:2 Author: 腾讯技术工程(查看原文) 阅读量:16 收藏
作者:foxxiao,腾讯 WXG 后开开发工程师
本文对完美 Hash 的概念进行了梳理,通过 Hash 构建步骤来了解它是如何解决 Hash 冲突的,并比较了 Hash 表和完美 Hash 表。下面介绍常见的 Hash 与 Perfect Hash 函数及它们在不同场景的应用。
散列函数(英语:Hash function)又称散列算法、哈希函数,是一种从任何一种数据中创建小的数字“指纹”的方法。散列函数把消息或数据压缩成摘要,使得数据量变小,将数据的格式固定下来。该函数将数据打乱混合,重新创建一个叫做散列值(hash values,hash codes,hash sums,或 hashes)的指纹。散列值通常用一个短的随机字母和数字组成的字符串来代表。
Hash 函数是一种将集合 S 转换成具有固定长度的、不可逆的的集合 U 的单射,它的值一般为数字合字母的组合,Hash 函数拥有无限的输入空间,却只有有限的输出空间,这意味着 Hash 函数一定会产生碰撞,一个好的 Hash 函数可以显著的降低碰撞概率。Hash 函数一般有一下特征:
一致性。Hash 函数可以接受任意大小的数据,并输出固定长度的散列值,同时输出不同值的概率应该尽可能一致。如 CityHash128,不管原始数据有多大,计算得到的 hash 值总是 128 bit。 雪崩效应。原始数据哪怕只有一个字节的修改,得到的 hash 值都会发生巨大的变化。 单向。只能从原始数据计算得到 hash 值,不能从 hash 值计算得到原始数据。所以散列算法不是加密解密算法,加密解密是可逆的,散列算法是不可逆的。 避免冲突。几乎不可能找到一个数据和当前计算的这个数据计算出一样的 hash 值,因此散列函数能够确保数据的唯一性。在 Hash 函数保证不同值出现的概率一致的情况下,CityHash128 出现碰撞的概率只有 2 ^ -128。因为不同 Key 的碰撞概率很小,所以在某些情况下我们可以直接使用较短的 Hash 值代替较长原始数据存储。
Hash 函数
常见的 Hash 函数有:
CRC32:CRC32 能够快速的生成 32 位 Hash 值,一般在数据库系统或数据传输中出现,用于快速校验数据是否完整; SipHash:SipHash 并不是为了速度设计的,与其他 Hash 函数相比速度上不占优势,而提供了 HashDoS 保护,是 Rust 中的 Hash 函数的默认实现,最新 Redis 中也在使用 SipHash; MurMurHash:经典快速的 Hash 函数,目前最新的版本是 MurMurHash3,可以生成 32 位或者 128 位 Hash 值; CityHash:来自于 Google 实现,受到 MurmurHash 启发,但是比 MurmurHash 更快,可以输出 64 位、128 位或者 256 位 Hash 值。ClickHouse 内置; xxHash:针对小数据集速度非常快,支持输出 32 位、64 位、128 位 Hash 值,Github 开源,SSE 支持。ClickHouse 内置。
xxHash 的 benchmark,统计了常用 Hash 函数的性能:
常见用法:
Hash 表:通过 Hash 算法将 Key 均匀映射到不同的位置上,访问单个 key 时可以达到 O(1) 的平均时间复杂度,加快访问速度。
安全 Hash 函数
安全 Hash 函数(或者叫加密 Hash 函数)是一种优秀的 Hash 函数,无法(或者很难)通过 Hash 值猜测出 Key,更精确的说,安全 Hash 必须满足抗碰撞和不可逆两个条件:无法通过 Hash 值的统计学方法逆向,以及无法通过算法层逆向。常见的安全 Hash 算法包括:
SHA2,SHA3 系列 BLAKE 系列
SHA0、SHA1、MD5 算法已经被认为是不安全的,存在已知的漏洞,不要使用这些不安全的 Hash 函数来签名。
常见用法:
安全 Hash 函数广泛应用于数字签名技术中:对原文进行 Hash 后,将 Hash 结果通过私钥签名,避免原文被泄露或者被修改;工作量证明:如加密货币中挖矿就是通过给定值,计算符合条件的 Hash 输入;文件 ID:在网站下载地址旁往往提供了文件的 MD5 或者 SHA-1,确保下载的文件完整且没有被调包。
HashDoS 与全域 Hash(universal hash)
全域 Hash 解决的是确定性 Hash 算法无法应对特殊输入的问题。在链式 HashMap 里,假设 m = bucket size,考虑我们有输入集合 S 和 Hash 函数 H,其中 H = H’ % m,攻击者在知道 Hash 函数的情况下,容易构造集合 S 使得集合中每一个元素的 Hash 值相同,那 HashMap 会退化成链表。最坏情况下,HashMap 查找的时间复杂度变成了 O(n),插入 n 个元素时需要 O(n2) 的时间复杂度,所以也叫 HashDoS 攻击。
全域 Hash 解决的问题是:对于精心构造的输入,冲突率仍然在 1 / m。一个简单的想法是随机选一个 Hash 函数,不是在每一次操作时选一个,而是在输入前选一个 Hash 函数,之后所有的操作都基于该 Hash 函数。
当然 H 也不是随便定义的,具体来说是在 |H| 个 Hash 函数 H 中随机的选择一个 Hash 函数作为所有 key 的 Hash 函数,H 中所有的 Hash 函数 H’ 对于不相等的关键词 x 和 y,使得 H’(x) 和 H’(y) 值相等的函数 H’ 的数量个数等于 |H| / m,此时冲突概率为 1/m。
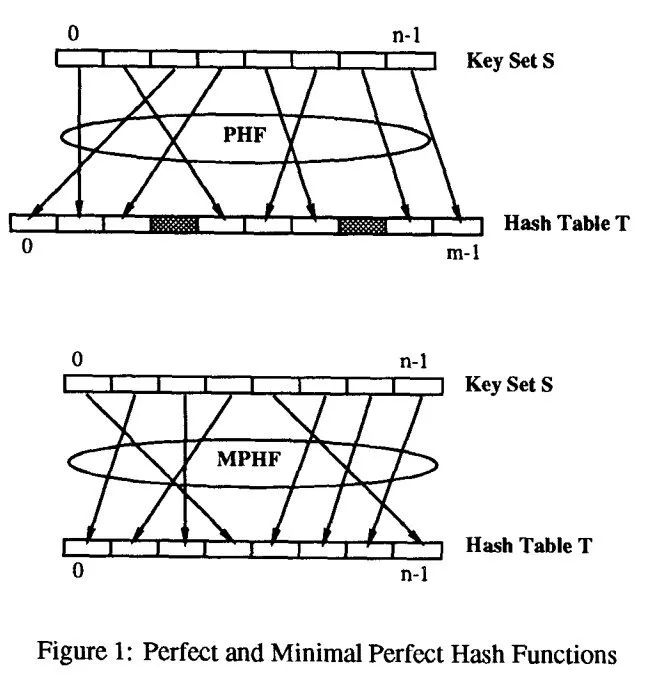
完美 Hash 函数
传统的 Hashmap 总会有分支预测开销与内存对比,最差时间复杂度是 O(n),有那么一种 Hash 函数:完美 Hash 函数( Perfect Hash Function,PHF),它可以在最坏情况下取得 O(1) 的时间复杂度。当然鱼和熊掌不可兼得,完美 Hash 要求有一个静态的输入集合,查找的 Key 必须存在于静态输入集合中,导致使用场景受限。它有几个特点:
完美 Hash 大部分都要求输入 Key 的集合是已知的,用于提前构建数据结构; 构造算法复杂,大部分情况下需要比较大的内存,特别是时间复杂度高,需要很长的时间建立索引,构建海量 key 的完美 Hash 可能会失败; 完美 Hash 在实现上并不是只有一个 Hash 函数,而是多个普通 Hash 函数与数据结构算法上的组合,这意味着需要额外空间存储 Hash 冲突信息。
尽管它有一些缺点,但是在一些场景如汉字拼音映射,词典,以及程序中预定义的映射关系都有它的应用。
Perfect Hash Function 对于给定的集合 S,可以将 S 中所有的 Key 映射到整数 [0, m) 中,其中 m >= |S|。当 m = |S| 时,称为最小完美 Hash 函数(Minimal Perfect Hash Function, MPHF)。即作为一个特例,如果完美 Hash 可以将 N 个 key 映射到 0 到 N-1 的整数,那它可以被称为最小完美 Hash 函数。
更进一步,如果 Hash 后给出 key 的顺序没有发生变化,称为完美 Hash 函数是保序的。如果一个 Hash 函数在给定区域不超过 t 次冲突,那这个 Hash 函数称为 t-完美 Hash 函数。
目前开源的 Perfect Hash 库有:
cmph:C/C++,集合了大部分知名完美 Hash 算法的库,针对不同的数据集合有推荐不同的算法,参数可调,文档不多,LGPL 协议 gperf:C/C++,专门针对于小数据集完美 Hash 的生成库,GPL 协议; rust-phf:使用 CHD 算法生成完美 Hash,使用简单,10 w 个 key 只需 0.4s 就能生成。
下文会讨论 FCH,CHD,PTHASH 是如何巧妙解决了 Hash 冲突并实现了最差 O(1) 时间复杂度的。
完美 Hash 首先需要离线构造得到 Hash 冲突的信息离线保存下来,需要查询时,利用先前生成的信息计算得到唯一的整数 Hash value。
在描述算法之前,先假设:
对于已知大小 n = |S| 的输入集合 S,已知的负载因子 alpha 和参数 c,table 的数量 table_size = n * alpha,桶的数量 m = cn / (log2 n + 1)。一般来说,c 在 2-8 左右,确保每个桶有合适数量的 key,同时不会空出太多的桶。最终所有的 key 会映射到 [0, table_size) 中的 整数。当 alpha = 1,table_size = n,为 MPHF。
FCH
A Faster Algorithm for Constructing Minimal Perfect Hash Functions 由 Fox, Chen, Heath 发明的一种生成完美 Hash 的算法,FCH 是一个相当经典的 Perfect Hash 的实现,后续多种算法均受到 FCH 算法的启发。
FCH 是一种基于二级 Hash 表的完美 Hash 函数:
将数据通过一级 Hash 映射到 T 空间中,然后冲突的数据随机选取新的哈希函数映射到 S 空间中,且 S 空间的大小 m 是冲突数据的平方(例如 T2 中有三个数字产生冲突,则映射到 m 为 9 的 S2 空间中,m 即为避免桶内 Hash 冲突的参数),此时可以容易找到避免碰撞的哈希函数(这个避免冲突的过程称为 position 或者 displace)。最差情况下所需存储空间为 O(n2),但只要适当选择哈希函数减少一级哈希时的碰撞,则可以使预期存储空间为 O(n)。
构造 FCH 需要分为三个步骤:
Mapping
Mapping 阶段为了将 60% 的 key 分布到 30 % 的桶里,将 n 个 key 分为 S1 和 S2 两个集合,其中 S1 称为 dense set,key 的数量大概保持在 0.6 * n,S2 为 sparse set,key 的数量大概在 0.4 * n 左右。同时,把所有桶分为两个部分 B1 和 B2,B1 数量 p2 = 0.3 * m,称为 dense buckets,B2 数量 0.7 * m,称为 sparse bucket。使用普通的 Hash 函数如 Cityhash/MurmurHash,将 S1 通过 H1 映射到 B1 中,同样道理将 S2 通过 H2 映射到 B2 中。
用数学语言描述:
Ordering
Ordering 阶段将所有的桶按照桶内冲突的数量排序,冲突数量最多的桶放在最前面。
Searching
Searching 阶段会依次处理每个桶里的冲突,尝试将不重复的 Hash 值分配给每一个 key。经过了上一个阶段排序,该阶段会优先处理冲突最多的桶。对于每一个桶,尝试参数 di, bi,给桶内每一个 key 分配 Hash 值 position(x, di, bi) = (h(x, s2 + b1) + di) mod table_size,这个值在 [0, table_size) 之间,其中 s2 是全局随机种子,bi 是单个 bit,di 是一个从 0 开始的递增的整数,如果 Hash 值在桶内和之前计算过的 Hash 值冲突,则改变 bi 或者 di 直到 Hash 值不发生冲突(为了加速 di 的寻找,原始论文中提出了辅助数据结构和压缩方法,感兴趣可以参考论文)。
处理完冲突后,最终可以得到 m 个参数 bi,di 存入 P 数组中,只占用大概 m * ((log2 n) + 1) = cn bit (这只是理论上的结果,如何存储 bi 和 di 不在我们讨论范围内),即每一个 key 只占用了 c 个 bit。
查询时:对于给定的 key,计算一级 Hash,得到桶编号,通过该桶的 bi,di 和全局 s2 参数来计算二级哈希,即完成了一次查找,可以发现,任何 key 的查询步骤都时相同的,没有循环,即所有步骤都是确定的 O(1)。注意到这里无法判断 key 是否存在。
在 FCH 中,c 越大,构造越快,但是空间利用率越低,特别是 FCH 寻找 MPHF 需要耗费巨量的时间:c = 3 时,1 亿 uint64 的数据需要花费 1 小时以上生成,所以它并不是一个实用的算法。
CHD
为了解决 FCH 构建过慢的问题,出现了基于 FCH 思想的 CHD,一种实现简单的 Perfect Hash 算法,支持 MPHF,空间利用率更高,但 lookup 更慢。
主要不同地方:使用通用 Hash 函数计算出为每一个 key 计算出三个 Hash 值:h, h0, h1,h 用来表示桶号,h0、h1 用来计算最终的 position,position 定义为 position = (h0 + (h1 * d1) + d0) mod table_size。
与 FCH 相同,CHD 一共分为三个阶段:
Mapping
Mapping 阶段不需要像 FCH 拆分两个集合,而是直接映射到一个集合中。
使用 c++ 来描述:
buckets.resize(m);
for (auto key : keys) {
auto [h, h0, h1] = hash(key);
buckets[h].hash = h;
buckets[h].keys.push_back(make_tuple(h0, h1));
}
Ordering
与 FCH 相同。
sort(buckets.begin(), buckets.end(), [](auto &lhs, auto &rhs){
return lhs.keys.size() > rhs.keys.size();
});
Searching (也叫 displace)
Searching 阶段同样是处理每个桶里的冲突,不同的是 position 函数发生了变化:为每一个桶初始化一个 pilot,其中 pilot = d0 * table_size + d1,使用 position 公式计算 key 的 Hash 值,发生冲突时,pilot 加上一(相当与 d1 加上 1,此时 position 的结果会发生较大的变化)重新计算 position 直到桶里所有 key 都不发生冲突。
bool_vector position_used, position_used_in_bucket;
vector<uint32> p; // 结果数组position_used.resize(table_size);
position_used_in_bucket.resize(buckets[0].keys.size());
p.resize(m);
for (auto &bucket : buckets) {
if (bucket.keys.size() == 0) continue;
// 单个桶 pilot = d0 * table_size + d1
int d0 = 0;
int d1 = 0;
while(true) {
bool ok = true;
position_used_in_bucket.clear();
for (auto [h0, h1] : bucket.keys) {
uint64 position = (h0 + (h1 * d1) + d0) % table_size;
if (position_used[position]) {
// hash 结果冲突,换一个 pilot
ok = false;
break;
}
if (position_used_in_bucket[position]) {
// 桶内 hash 结果冲突,换一个 pilot
ok = false;
break;
}
position_used_in_bucket[position] = true;
}
if (ok) {
// 单个桶处理完毕
position_used.union(position_used_in_bucket);
// pilot 存到 p 数组中
p[bucket.h] = d0 * table_size + d1;
break;
}
d1++;
if (d1 >= table_size) {
d1 = 0;
d0++;
if (d0 > table_size) {
// 构建失败,找不到一个可用的 pilot
throw ...
}
}
}
}
最终得到的 m 个 pilot 存入 P 数组中。
查询时:对于给定的 key,使用固定出的 Hash 函数计算出 h, h0, h1,根据 P[h] 得到 pilot 与 d0, d1,使用 poisition 易求得 Hash 值,即完成了一次查找(至少 4 次除法 or 求余操作,h < m)
auto [h, h0, h1] = hash(key);
auto pilot = p[h];
auto d0 = pilot / table_size;
auto d1 = pilot % table_size;
return (h0 + (h1 * d1) + d0) % table_size;
结果集 P 中,pilot 往往很小,有压缩空间,在作者的论文中,为了压缩 P 数组的大小,采用 FN Encoding,可以压缩到 2.08 bit/key 的开销,自己的实现可以直接用 bit vector(aka compact) 压缩,实现起来更简单。
compact 压缩:给定一系列整数 S,已知 S 中最大的整数 x 需要使用 y 个 bit 表示,我们可以将所有的整数都通过固定 y bit 来表示而不牺牲精度和访问时间。
CHD 算法比较简单,Github 上也有不同语言的实现, rust 语言的实现。Go 语言实现。
PTHash
虽然 CHD 实现简单,但其中包含了大量除法求余计算,Encoding 后效率并不高,lookup 耗时过久。最近有一篇文章提出了 PTHash 方法,在 FCH 上改进了构建时间,并提高了空间利用率,作者还提供了源代码供参考。
设计思路和 FCH 相似,只不过 position 定义变成了 position(x, pilot) = (h(x, s) xor h(pilot, s)) mod table_size,其中 h 是普通 Hash 函数,x 是 key,s 是全局种子。与 FCH 相比可以提前计算所有 key 的 Hash h(x, s),节约构造时间 。使用 compact 压缩方式效果很好,lookup 耗时也能达到 FCH 水平。
Mapping
与 FCH 相同
Ordering
与 FCH 相同
Searching
使用新的公式计算 position,得到 n 个 pilot,由 position 公式定义,可以发现大部分 pilot 都是比较小的值,作者还介绍了一种 Front-Back Encoding,将结果集前 30% 拆分成 front 集,后 (1- 30%) 拆分为 back 集,代价是运行时多一次分支判断。
由于 front 集合里的桶是最先处理冲突的,冲突发生次数低,大部分 pilot 都比 back 集合内的要小,压缩率更高。将 Front 和 Back 集合里的 pilot 通过 Compact 编码后,称为 Compact-Compact Encoding。
查询时,按照 bucket id 确定去 front 还是 back 集合查询 pilot,不考虑解压过程,只需要两次除法 or 求余操作。
当然这里也可以牺牲部分空间,不做 Front-Back Encoding 以取得更快的查询速度,根据不同的 Encoding 方式,可以在时间&空间上取得平衡:
HashMap
HashMap 本质上是根据给定的 key 获得 value 的地址。设计核心主要在于:
HashMap 的空间开销:key 和 value 如何组织?单个 key 需要多少额外空间存储元信息? HashMap 的查询与插入:如何通过 key 计算出 value 的地址?冲突如何处理? 不同的 HashMap 不同点在于冲突如何处理,除了常规可读可写的 HashMap,存在只读 HashMap,存储更小,性能更优。
常规 HashMap
在各个语言都有内置的 HashMap 实现,除了使用不同的 Hash 函数,不同实现对 Hash 冲突的解决方案也不同:
拉链法:每一个桶都存着链表的 head 节点,冲突 key 将会被插入链表; 升级红黑树:Java8 在链表长度超过 8 时转换成红黑树; 线性探测法:发现冲突时向后找到第一个没有占用的桶存储,缓存命中率高,负载因子越高,插入效率越低; 多级 Hash 法:单次 Hash 结果冲突时,换一个 Hash 函数直到 Hash 值无冲突。
F14 & B16 系列 HashMap
F14 & B16 是一种利用 SIMD 技术进行查找的链式 HashMap,它为每一个 Key 计算两个 Hash 值:H1 和 H2,H1 决定 Key 放在哪一个桶里,H2 用来处理桶内冲突,一般要求负载因子比较高,以获得较高的空间利用率。同时对桶内的 H2 通过 SIMD 指令对比,一次对比 14 个 key 或者 16 个 key,相比 PerfectHashMap,它可以支持动态插入,但是查找性能不如 PerfectHashMap。
PerfectHashMap
有没有办法把 Prefect Hash 利用起来做 HashMap?由于 Perfect Hash 已经映射到 [0, table_size) 内的整数,完全不需要考虑 key 的冲突处理,所以想用起来比较简单:
当 hashmap 的 value 定长时,我们可以直接通过 Hash 值(Index)计算出 value 的 offset,无需使用任何额外空间。 当 hashmap 的 value 不定长时,引入一层 relocation,存储每一个 Hash 值对应 value 的 offset,由于 Hash 值是从 0 递增的,因此 offset 也是递增的,可以通过一定方法去压缩 value offset。
完美 Hash 要求查询的 key 需要存在于输入集内,其他 HashMap 没有这么苛刻的要求,如果使用一个不在输入集中的 key 会怎么样呢?从 CHD 算法的 lookup 过程来分析,输入未知 key 时可以认为返回一个随机的 Index,如果我们需要确认 key 是否存在 HashMap 里,需要将原始 key 存下来放在 Index 对应的 Value 中,查询到 Index 后再对比一次才能确认 key 是否存在。
PerfectHashMap 一般用法是先离线生成 map 信息,再读到 buffer 里,或者像 rust-phf 一样编译时内置到二进制,直接读 P 数组,如果 HashMap 特别大,还可以通过 mmap 只读方式载入到内存中。
Benchmark
测试设备:MacBookPro m1 Pro 32G,MacOS 12.4,clang 13.1.6。
比较对象:
unordered_map:标准库自带的 HashMap,链式实现; Folly F14:Facebook HashMap 实现,使用 SIMD 优化查询过程; abseil swiss table:Google HashMap 实现,为速度优化,包括使用额外指针的 node_hash_map,与原地存储适合小 value 的 flat_hash_map; PTHashMap:PTHash + Value offset 映射,(内部使用 CityHash128),c = 7, alpha = 0.98,Compact-Compact Encoding,Value offset 使用 MILC 压缩。不存储 key; PTHashMap3:与 PTHashMap 参数不同:c = 3, alpha=0.99; PTHashMap10:与 PTHashMap 参数不同:c = 10, alpha=0.94。
string
测试场景:输入 100w 随机不重复不定长字符串(平均长度 8 bytes)作为 key,value 与 key 相同。全部随机 lookup 一遍。
meta data 排除了 key 和 Value 之后统计占用内存大小,folly 使用 computeStats() 统计内存数据;total memory 值插入所有 key 后使用 gpertools 统计占用内存大小,包含 key 和 value 部分;注意 PTHashMap meta data 统计单位是 bit。
uint64
测试场景:输入 100w 随机不重复 uint64 数字作为 key,value 与 key 相同,全部随机 lookup 一遍。
由于该场景数据是长度固定,PTHashMap 去掉了 Value offset 映射表。
结论
完美 Hash 的概念扩展了 Hash 的使用场景,最近出现的新型完美 Hash 算法在运行速度&构建速度上取得了较大的进步,针对海量只读场景使用完美 HashMap 不仅可以提升速度,同时能够节省大量内存占用。
参考文章
如有侵权请联系:admin#unsafe.sh