这是编程珠玑上面的一个题,也是笔试中出烂了的题目。题目非常简单,描述如下:将一个n元一维向量向左旋转i个位置,例如当n=8,i=3时,向量abcdefgh旋转为defghabc。简单的代码使用一个n元的中间向量在n步内完成该工作。你能否仅使用额外字节的存储空间,在正比于n的时间内完成向量的旋转?
下面是最简单的一种解法。
#include <iostream>
using namespace std;
void reverse(char *a,int beg, int end)
{
char tmp;
for (; beg < end; beg++, end-- )
{
tmp = a[beg];
a[beg] = a[end];
a[end] = tmp;
}
}
void LeftReverse(char *a,int n, int k)
{
reverse(a,0,k - 1);
reverse(a,k,n - 1 );
reverse(a,0,n - 1);
}
int main()
{
char test[] = "123abcdefg" ;
LeftReverse(test,strlen(test),3);
printf( "reversed:%s",test);
return 0;
}
当然,今天的主题不是这个,而是书中提到的另一种解法:英文是啥给忘了,翻译成“杂耍算法”。这个算法的步骤是这样的:move x[0] to the temporary t, then move x[i] to x[0], x[2i] to x[i], and so on, until we come back to taking an element from x[0], at which point we instead take the element from t and stop the process. If that process didn’t move all the elements , then we start over at x[1], and continue until we move all the elements.具体代码如下:
#include <iostream>
using namespace std;
int gcd(int a,int b)
{
int c;
if (a < b)
{
c = a;
a = b;
b = c;
}
while(b)
{
if(a % b == 0)
return b;
else
{
c = a % b;
a = b;
b = c;
}
}
}
void rotate(char * a,int n, int k)
{
char tmp;
int j;
for (int i = 0; i < gcd(n,k); ++i)
{
tmp = a[i];
for (j = i + k; j!= i; j = (j + k) % n)
{
a[(j-k+n) % n] = a[j];
}
j = (j - k + n ) % n;
a[j] = tmp;
}
}
int main()
{
char a[] = "abc12345678" ;
cout << "gcd(11,3):" << gcd(11,3) << endl;
rotate(a,11,3);
printf ( "after rotate:%s\n",a);
return 0;
}
经过如下图所示的步骤之后,就完成了移位,此例中i=3,n=11。
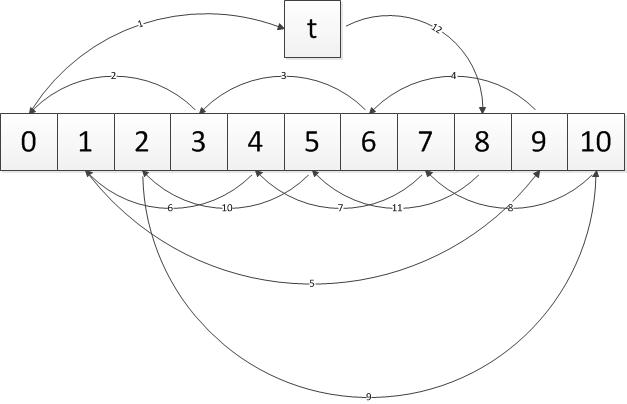
这个算法会在执行\(gcd(i,n)\)次后就停止了,为什么?这就涉及到数论知识了,也就是今天的主题。
数论中有这样一个结论:\(n\)个数
\[0\,mod\,n,\quad i\,mod\,n,\quad 2i\,mod\,n,\quad \cdots,\quad (n-1)i\,mod\,n\quad (1)\]
按照某种次序恰好组成\(\frac{n}{d}\)个数
\[0,\quad d,\quad 2d,\quad \cdots,\quad n-d\quad \quad (1)\]
的\(d\)份复制,其中\(d=gcd(i,n)\).例如,当\(n=12\)且\(i= 8\)时,有\(d=4\),这些数就是\(0,8,4,0,8,4,0,8,4,0,8,4\).
证明(指出我们得到前面\(\frac{n}{d}\)个值的\(d\)份复制)的第一部分是显然的,根据同余式的基本理论,我们有
\[ji\equiv ki(mod\,n)\Leftrightarrow j\frac{i}{d}\equiv k\frac{i}{d}(mod\,\frac{n}{d})\]
可以看到当\(0\leqslant k< \frac{n}{d}\)时,我们得到了就是这\(\frac{n}{d}\)个数的\(d\)份复制,\(k\)的取值就是模数为\(\frac{n}{d}\)的最小完全非负剩余系中的数。
现在证明这\(\frac{n}{d}\)个数就是\({0,d,2d,\cdots,n-d}\)(按照某种次序排列)。记\(i={i}'d,n={n}'d\).根据mod的分配率\(c(x\,mod\,y)=(cx)\,mod\,(cy)\),就有
\[ki\,mod\,n=d(k{i}'\,mod\,{n}')\]
所以当\(0\leqslant k< {n}'\)时出现的那些值就是\(d\)乘以以下诸数
\[0\,mod\,{n}',\quad {i}'\,mod\,{n}',\quad {2{i}'}\,mod\,{n}',({n}'-1){i}'\,mod\,{n}'\]
我们知道\(({i}',{n}')=1\),所以我们只需要证明\(d=1\)的情况,也就是\(i\)与\(n\)互素的情况。
现在我们假设\((i,n)=1\),(1)式中的数是各不相同的,如若不然,取\(k,j\in [0,n-1],k\neq j\),假设\(ki=ji\),则有\(ki\equiv ji(mod\,n)\)。由于\((i,n)=1\),则\(k\equiv j(mod\,n)\),所以\(k=j\),显然矛盾。所以(1)中的数恰好就是\(0,1,2,\cdots,n-1\)
结论证完,下面回到例子简要分析,在本例中\(n=11,i=3,gcd(11,3)=1\),于是
\[0,3\,mod\,11,6\,mod\,11,\cdots,10*3\,mod\,11\]
的值恰好就是\(11\)的最小非负完全剩余系按一定顺序 排列的结果。所以经过如下的步骤
t = x[0]
x[0] = x[i mod n]
x[i mod n] = x[2i mod n]
……
x[(n-2)*i mod n] = x[(n-1)*i mod n]
x[(n-1)*i mod n] = t
之后,所有的元素都到了该去的地方,
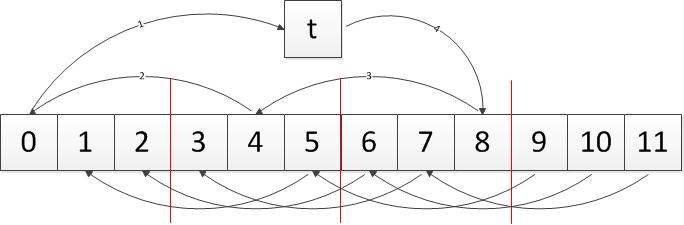
当\((n,i)=d(d\neq 1)\)怎么办呢。从上面的结论我们可以知道每隔\({n}'=\frac{n}{d}\)之后,序列会从\(0,d,2d,\cdots,{n}'-d\)的某个序列重新开始,这样我们就又遇到\(x[0]\)了。这个时候我们需要将\(x[1]\)移到\(t\),重复上述步骤,我们简要看看图示。
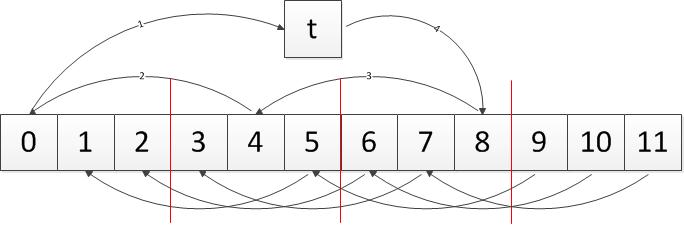
看看图示就明了了。
这是复习数论的时候遇到的一个结论,然后想起曾经的一个题。现在确实是完全清晰了。人说,数学是科学的女皇,数论是数学的女皇,数论里面充满着迷人的结论。这世间充满了美妙,我希望能够与诸君分享。
如有侵权请联系:admin#unsafe.sh