前言
因为数据结构和算法这一块的知识比较匮乏,很多东西都是只有一个模糊的概念,并不知其所以然,其实很早就想学习数据结构和算法,但是由于很多原因(懒)一直没有真正的行动起来,学起来也是东一榔头西一棒槌,很乱,这次准备开始系统的学习数据结构和算法。
Github 地址:https://github.com/her-cat/learning-datastructure-algorithm
数据结构相关知识
数据结构
数据结构是指数据元素之间存在着一种或多种关系的集合,简单来说就是 一组数据的存储结构。
逻辑结构
数据的逻辑结构分为四种:
- 集合结构:数据元素之间没有任何联系,只是
属于同一个集合。 - 线性结构:数据元素之间存在一对一的序关系。
- 树结构:数据元素之间存在一对多关系。
- 图结构:也称网状结构,数据元素之间存在多对多关系。
物理结构
数据的物理结构分为四种:
- 顺序存储结构:用
物理位置的相邻关系表示数据元素之间的逻辑关系。 - 链式存储结构:对每一个数据元素用一块较小的连续区域存放,称为节点,然后用指针表示逻辑关系,在节点中设置一个或多个指针,指向它的前驱或后继元素的地址。
- 索引存储结构:这是一种顺序加链式的存储方式,数据元素按顺序结构存放,然后将每个数据元素的关键字和存储地址构造一个索引表单独储存,这种存储结构
不表示元素之间的关系。 - 哈希存储结构:数据元素按顺序或链式存储,并在数据元素的关键字与存储地址之间建立一种映射,这种存储结构
不表示元素之间的关系。
什么是栈
栈是限定只能在表的一端进行插入或删除操作的线性表。
线性表:相同类型的数据的有限序列。
允许插入、删除操作的一端是栈顶、另一端是栈顶。
一般将插入和删除操作称为入栈和出栈。
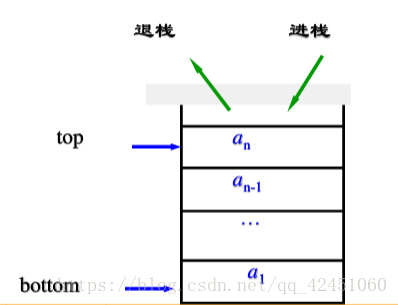
现实生活中有很多类似于栈的操作,比如洗碗的时候,将洗干净的碗一个接一个的往上放(相当于入栈),取碗时,则从上面一个接一个往下取(相当于出栈)。
我们放碗的顺序是12345、取碗的顺序是54321,放碗的时候必须按照从下往上的顺序放,不能先放上面的再放下面的,取得时候必须从上往下取。
特点:限制在表的一端操作,后入先出(LIFO,即 Last In First Out)
顺序栈和链栈
栈是一种线性表,所以栈也有线性表的两种存储结构(顺序存储结构和链式存储结构)。
栈的顺序存储结构称为顺序栈,链式存储结构称为链栈。
顺序栈
利用一组地址连续的存储单元依次存放栈底到栈顶的数据元素,栈底位置固定不变,栈顶位置随着入栈和出栈操作而变化。
链栈
链栈是一种特殊的线性链表,和所有链表一样,是动态存储结构,无需预先分配存储空间。
栈的操作
顺序栈和链栈的存储方式不同,所以对栈的操作的实现方式也不一样,一般栈有以下几个基本操作。
- InitStack(初始化栈)
- IsEmpty(是否为空栈)
- IsFull(是否已满栈)
- Push(入栈)
- Pop(出栈)
- GetTop(获取栈顶)
下面分别演示顺序栈和链栈的操作。
顺序栈
栈的定义
#define FALSE 0
#define TRUE 1
#define STACK_SIZE 50
#define STACK_ELEMENT_TYPE int
/* 顺序栈结构体类型 */
typedef struct
{
/* 用于存放栈中元素的一维数组 */
STACK_ELEMENT_TYPE elem[STACK_SIZE];
/* 用来存放栈顶元素的下标 */
int top;
} SeqStack;
FALSE 和 TRUE 即 假和真, STACK_SIZE 是栈的大小,STACK_ELEMENT_TYPE 是栈中数据元素的类型,elem 用来存放数据元素,top 用于存放栈顶元素的下标。
初始化栈
void InitStack(SeqStack *S)
{
/* top为-1表示空栈 */
S->top = -1;
}
栈顶元素下标 top 等于 -1 为空栈,所以只需将 top 赋值 -1 即可完成顺序栈的初始化。
是否为空栈
int IsEmpty(SeqStack *S)
{
if (S->top == -1) {
return TRUE;
} else {
return FALSE;
}
}
如果栈顶元素下标 top 等于 -1,则栈是空栈。
是否已满栈
int IsFull(SeqStack *S)
{
if (S->top == STACK_SIZE - 1) {
return TRUE;
} else {
return FALSE;
}
}
如果栈顶元素下标 top 等于栈的大小(STACK_SIZE - 1),则栈已满。
入栈
int Push(SeqStack *S, STACK_ELEMENT_TYPE value)
{
if (IsFull(S) == TRUE) {
// 栈已满
return FALSE;
}
// 修改栈顶元素下标
S->top++;
S->elem[S->top] = value;
return TRUE;
}
先判断是否已经满栈,然后移动栈顶元素下标,再将数据放入栈中。
出栈
int Pop(SeqStack *S, STACK_ELEMENT_TYPE *value)
{
if(IsEmpty(S) == TRUE) {
// 栈为空
return FALSE;
}
*value = S->elem[S->top];
// 修改栈顶元素下标
S->top--;
return TRUE;
}
先判断栈是否为空,然后将栈顶元素下标对应的数据取出来,移动栈顶元素下标。
获取栈顶
int GetTop(SeqStack *S, STACK_ELEMENT_TYPE *value)
{
if(IsEmpty(S) == TRUE) {
return FALSE;
}
*value = S->elem[S->top];
return TRUE;
}
跟出栈的逻辑一样,只是没有移动栈顶元素的下标。
链栈
栈的定义
#define FALSE 0
#define TRUE 1
#define STACK_ELEMENT_TYPE int
/* 链栈节点 */
typedef struct node {
STACK_ELEMENT_TYPE data;
struct node *next;
} LinkStackNode;
/* 链栈结构 */
typedef struct {
LinkStackNode *top;
int length;
} LinkStack;
data 存放的是数据元素,*next 是后继节点的指针,*top 是栈顶,插入和删除都是在这里,length 是链栈的长度。
初始化栈
void InitStack(LinkStack *S)
{
S->top = NULL;
S->length = 0;
}
初始化栈顶指针和链栈长度。
是否为空栈
int IsEmpty(LinkStack *S)
{
if (S->length == 0) {
return TRUE;
} else {
return FALSE;
}
}
当链栈长度等于0的时候为空栈,也可以判断 top 是否为 NULL;
入栈
int Push(LinkStack *S, STACK_ELEMENT_TYPE value)
{
LinkStackNode *temp = (LinkStackNode *)malloc(sizeof(LinkStackNode));
if (temp == NULL) {
// 申请空间失败
return FALSE;
}
temp->data = value;
temp->next = S->top;
// 将新元素作为栈顶指针
S->top = temp;
// 链栈长度加一
S->length++;
return TRUE;
}
首先将栈顶 top 赋值给 temp->next,然后将 temp 作为栈顶指针,链栈长度加一。
出栈
int Pop(LinkStack *S, STACK_ELEMENT_TYPE *value)
{
if (IsEmpty(S) == TRUE) {
// 空栈
return FALSE;
}
LinkStackNode *temp = S->top;
// 移动栈顶指针
S->top = temp->next;
// 链栈长度减一
S->length--;
// 将链栈元素返回
*value = temp->data;
// 释放temp空间
free(temp);
return TRUE;
}
上面已经说过,链栈的插入、删除操作都是在操作 top,所以我们先将 top 取出来赋值给 temp,然后将栈顶元素的后继节点作为栈顶,链栈长度减一,取出旧的栈顶中的数据(注意这里是 temp->data,而不是 S->top->data),然后释放旧的栈顶元素。
获取栈顶
int GetTop(LinkStack *S, STACK_ELEMENT_TYPE *value)
{
if(IsEmpty(S) == TRUE) {
return FALSE;
}
*value = S->top->data;
return TRUE;
}
如果不是空栈,直接取栈顶元素中的数据就可以了。
栈的应用
接下来就用栈相关的知识进行实际应用。
在 leetcode 中一道题目叫做 有效的括号,题目的内容:
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
输入: "()"
输出: true
输入: "()[]{}"
输出: true
输入: "(]"
输出: false
输入: "{[]}"
输出: true
题目分析:在文章开始的时候,举了一个洗碗的例子,放碗的顺序是12345、取碗的顺序是54321,如果将 12345 看成五种括号,那么我们放碗和取碗的顺序就是一个有效的括号(1234554321),所以这题可以用栈来解决.
代码:
bool isValid(char* s) {
char ch;
InitStack(&S);
for (int i = 0; i < strlen(s); ++i) {
// 如果当前字符是左括号则入栈
if (s[i] == '(' || s[i] == '{' || s[i] == '[') {
Push(&S, s[i]);
} else if (s[i] == ')') {
Pop(&S, &ch);
if (ch != '(') {
return 0;
}
} else if (s[i] == '}') {
Pop(&S, &ch);
if (ch != '{') {
return 0;
}
} else if (s[i] == ']') {
Pop(&S, &ch);
if (ch != '[') {
return 0;
}
}
}
if (IsEmpty(&S) == FALSE) {
return 0;
}
return 1;
}
s 就是我们需要检验的字符串, ch 用来存放取出来的括号,先初始化栈,然后使用for循环遍历整个字符串,s[i] 是当前遍历到的括号,当 s[i] 中的括号是左括号时,将括号入栈。当s[i]中的括号为右括号,我们需要出栈一个括号,然后判断出栈的括号是不是与当前遍历到的括号相匹配,比如当前遍历到的括号是 ),那么我们出栈的括号必须是 (,最后需要判断一下栈中是否还有括号,如果栈中还有括号,就说明这个字符串不是有效的括号,因为括号都是成双成对出现的,如果是有效的括号,就不会存在栈中还有括号存在。
总结
凡是满足只能在一端进行插入、删除操作,并且是后入先出的,我们都可以称它为栈。
最后,祝大家中秋节快乐!